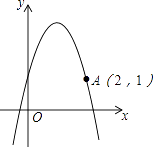题目内容
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论
①a>0,②b>0,③c>0,④b2﹣4ac>0
其中正确的有( )
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】解:①∵该二次函数图象的开口方向向下,
∴a<0;
故本选项错误;
②∵该图象的对称轴x=﹣ ![]() >0,
>0,
∴b>0;
故本选项正确;
③∵该函数图象与y轴交于正半轴,
∴c>0;
故本选项正确;
④该二次函数的图象与x轴有2个不相同的交点,依据根的判别式可知b2﹣4ac>0;
故本选项正确;
综上所述,正确的说法是:②③④,共有3个;
故选C.
【考点精析】认真审题,首先需要了解二次函数图象以及系数a、b、c的关系(二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)).

练习册系列答案
相关题目
【题目】阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.
组别 | 时间(小时) | 频数(人数) | 频率 |
A | 0≤t≤0.5 | 6 | 0.15 |
B | 0.5≤t≤1 | a | 0.3 |
C | 1≤t≤1.5 | 10 | 0.25 |
D | 1.5≤t≤2 | 8 | b |
E | 2≤t≤2.5 | 4 | 0.1 |
合计 | 1 |
请根据图表中的信息,解答下列问题:
(1)表中的a= ,b= ,中位数落在 组,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生大约有多少名?
(3)E组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.