题目内容
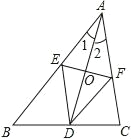
【题目】如图,矩形ABCD中,O是对角线AC的中点,延长AB到G,使BG=AB,连接GO并延长,交BC于E,交AD于F,且AC=2AB,连接AE、CF.求证:四边形AECF是菱形.
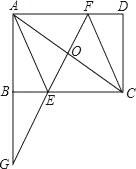
【答案】见解析
【解析】
连接CG,推出∠ACB=30°,∠BAC=60°,证△ACG是等边三角形,得到AG=CG,推出EF⊥AC,证△AOF≌△COE,推出CE=AF,根据菱形的判定得到四边形AECF是菱形即可.
证明:连接CG,
∵在矩形ABCD中AC=2AB,
∴∠CAG=60°,
∵BG=AB,
∴AG=AC,
∴△ACG是等边三角形,
∵O为AC的中点,
∴GF⊥AC,
∵在矩形ABCD中,BC‖AD,
∴∠DAC=∠BCA,AO=OC,∠AOF=∠COE=90°,
∴△AOF≌△COE,
∴CE=AF,
∴四边形AECF是平行四边形,
∴四边形AECF是菱形(对角线互相垂直的平行四边形是菱形).

练习册系列答案
相关题目