��Ŀ����
��ͼ�����κ���y=ax2+x+c��ͼ����x�ύ�ڵ�A��B���㣬��A������Ϊ��-2��0����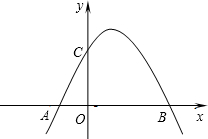 ��y�ύ�ڵ�C��0��3����
��y�ύ�ڵ�C��0��3����
��1�����������κ����Ľ���ʽ��
��2��ֱ��д����B������Ϊ________��
��3����x���Ƿ����һ��P��ʹ��ACP�ǵ��������Σ������ڣ��������������P�����ꣻ�������ڣ���˵�����ɣ�
��4���ڵ�һ�����е����������Ƿ����һ��Q��ʹ���ı���ABQC�������������ڣ������Q�����꼰��������ֵ���������ڣ���˵�����ɣ�
 �⣺��1����y=ax2+x+c��ͼ��A��-2��0����C��0��3����
�⣺��1����y=ax2+x+c��ͼ��A��-2��0����C��0��3������c=3��a=-
 ��
�����������ʽΪ��y=-
 x2+x+3��
x2+x+3����������κ����Ľ���ʽ��y=-
 x2+x+3��
x2+x+3����2���⣺��6��0����
�ʴ�Ϊ����6��0����
��3���⣺��Rt��AOC�У�
��AO=2��OC=3����AC=
 ��
�����ٵ�P1A=ACʱ��P1��x��ĸ����ᣩ��P1��-2-
 ��0����
��0�����ڵ�P2A=ACʱ��P2��x��������ᣩ��P2��
 -2��0����
-2��0�����۵�P3C=ACʱ��P3��x��������ᣩ��P3��2��0����
�ܵ�P4C=P4Aʱ��P4��x��������ᣩ��
��Rt��P4OC����P4O=x����x+2��2=x2+32
��ã�x=
 ��
����P4��
 ��0����
��0��������x�����һ��P��ʹ��ACP�ǵ��������Σ�����������P�������ǣ�-2-
 ��0����
��0���� -2��0����2��0����
-2��0����2��0���� ��0����
��0������4���⣺��ͼ����Q������Ϊ��x��y������Ϊ��Q��y=-
 x2+x+3�ϣ�
x2+x+3�ϣ�����Q������Ϊ��x��-
 x2+x+3����
x2+x+3��������OQ��
S�ı���ABQC=S��AOC+S��OQC+S��OBQ��
=3+
 x+3��-
x+3��- x2+x+3��
x2+x+3��=-
 x2+
x2+ x+12��
x+12����a��0��
��S�ı���ABQC���ֵ=
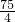 ��
��Q��������3��
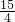 ����
�������ڵ�һ�����е��������ϴ���һ��Q��ʹ���ı���ABQC��������Q�������ǣ�3��
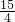 ������������ֵ��
������������ֵ��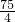 ��
����������1����Ϊy=ax2+x+c��ͼ��A��-2��0����C��0��3�����������c��a��ֵ�����ɵõ��𰸣�
��2����y=0�������x��ֵ�����ɵõ��𰸣�
��3����Rt��AOC�и��ݹ��ɶ������AC�����ݵ��������ε�����������ٵ�P1A=ACʱ��P1��x��ĸ����ᣩ��P1��-2-
 ��0�����ڵ�P2A=ACʱ��P2��x��������ᣩ��P2��
��0�����ڵ�P2A=ACʱ��P2��x��������ᣩ��P2�� -2��0�����۵�P3C=ACʱ��P3��x��������ᣩ��P3��2��0�����ܵ�P4C=P4Aʱ��P4��x��������ᣩ��P4��
-2��0�����۵�P3C=ACʱ��P3��x��������ᣩ��P3��2��0�����ܵ�P4C=P4Aʱ��P4��x��������ᣩ��P4�� ��0�������ɵó��𰸣�
��0�������ɵó��𰸣���4����Q������Ϊ��x��y������Ϊ��Q��y=-
 x2+x+3�ϣ��ó�Q������Ϊ��x��-
x2+x+3�ϣ��ó�Q������Ϊ��x��- x2+x+3��������OQ������S�ı���ABQC=S��AOC+S��OQC+S��OBQ������������ɣ�
x2+x+3��������OQ������S�ı���ABQC=S��AOC+S��OQC+S��OBQ������������ɣ�������������Ҫ������ô���ϵ��������κ����Ľ���ʽ�����������ε��ж��������ε���������κ���ͼ���ϵ���������������κ�������ֵ��֪ʶ�����������գ��ۺ�������Щ���ʽ��м����ǽ����Ĺؼ������ͽϺã��ۺ���ǿ��

��ϰ��ϵ�д�
�����Ŀ
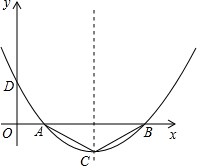 ��ͼ�����κ�����ͼ����D��0��
��ͼ�����κ�����ͼ����D��0��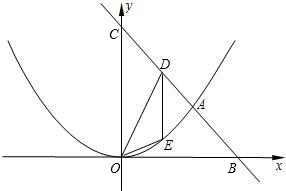
 ��ͼ�����κ���y=ax2+bx+c��ͼ����x�ύ��B��C���㣬��y�ύ�ڵ�A��0��-3������ABC=45�㣬��ACB=60�㣬��������κ�������ʽ��
��ͼ�����κ���y=ax2+bx+c��ͼ����x�ύ��B��C���㣬��y�ύ�ڵ�A��0��-3������ABC=45�㣬��ACB=60�㣬��������κ�������ʽ��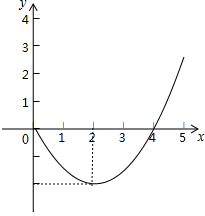 ij��˾�Ƴ���һ�ָ�Ч������ϴ����Ʒ��������к�˾�����˴ӿ���ӯ���Ĺ��̣���ͼ�Ķ��κ���ͼ���֣��̻��˸ù�˾��������ۻ�����s����Ԫ����ʱ��t���£�֮��Ĺ�ϵ����ǰt���µ������ܺ�s��t֮��Ĺ�ϵ��������ͼ���ṩ����Ϣ������������⣺
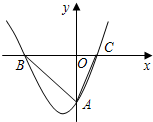
ij��˾�Ƴ���һ�ָ�Ч������ϴ����Ʒ��������к�˾�����˴ӿ���ӯ���Ĺ��̣���ͼ�Ķ��κ���ͼ���֣��̻��˸ù�˾��������ۻ�����s����Ԫ����ʱ��t���£�֮��Ĺ�ϵ����ǰt���µ������ܺ�s��t֮��Ĺ�ϵ��������ͼ���ṩ����Ϣ������������⣺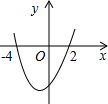 ��ͼ�����κ���y=ax2+bx+c��ͼ����x���ཻ�������㣬����ͼ��ش𣺣�1��b
��ͼ�����κ���y=ax2+bx+c��ͼ����x���ཻ�������㣬����ͼ��ش𣺣�1��b