题目内容
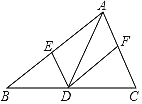
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(﹣2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.
【答案】
(1)
解:将点B,点C的坐标分别代入y=ax2+bx+4可得 ![]() ,解得
,解得 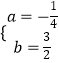 ,
,
∴二次函数的表达式为y=﹣ ![]() x2+
x2+ ![]() x+4
x+4
(2)
解:设点N的坐标为(n,0)(﹣2<n<8),
则BN=n+2,CN=8﹣n.
∵B(﹣2,0),C(8,0),
∴BC=10,
在y=﹣ ![]() x2+
x2+ ![]() x+4中令x=0,可解得y=4,
x+4中令x=0,可解得y=4,
∴点A(0,4),OA=4,
∴S△ABN= ![]() BNOA=
BNOA= ![]() (n+2)×4=2(n+2),
(n+2)×4=2(n+2),
∵MN∥AC,
∴ ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() ,
,
∵﹣ ![]() <0,
<0,
∴当n=3时,即N(3,0)时,△AMN的面积最大
(3)
解:当N(3,0)时,N为BC边中点,
∵MN∥AC,
∴M为AB边中点,
∴OM= ![]() AB,
AB,
∵AB= ![]() =
= ![]() =2
=2 ![]() ,AC=
,AC= ![]() =
= ![]() =4
=4 ![]() ,
,
∴AB= ![]() AC,
AC,
∴OM= ![]() AC
AC
【解析】(1)由B、C的坐标,利用待定系数法可求得抛物线解析式;(2)可设N(n,0),则可用n表示出△ABN的面积,由NM∥AC,可求得 ![]() ,则可用n表示出△AMN的面积,再利用二次函数的性质可求得其面积最大时n的值,即可求得N点的坐标;(3)由N点坐标可求得M点为AB的中点,由直角三角形的性质可得OM=
,则可用n表示出△AMN的面积,再利用二次函数的性质可求得其面积最大时n的值,即可求得N点的坐标;(3)由N点坐标可求得M点为AB的中点,由直角三角形的性质可得OM= ![]() AB,在Rt△AOB和Rt△AOC中可分别求得AB和AC的长,可求得AB与AC的关系,从而可得到OM和AC的数量关系.
AB,在Rt△AOB和Rt△AOC中可分别求得AB和AC的长,可求得AB与AC的关系,从而可得到OM和AC的数量关系.
【考点精析】解答此题的关键在于理解二次函数图象以及系数a、b、c的关系的相关知识,掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).

 科学实验活动册系列答案
科学实验活动册系列答案【题目】某校决定组织学生开展校外拓展活动,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.现有甲乙两种大客车,它们的载客量和租金如下表所示.学校计划此次拓展活动的租车总费用不超过3100元,为了安全,每辆客车上至少要有2名老师.
客车 | 甲种 | 乙种 |
载客量/(人/辆) | 30 | 42 |
租 金/(元/辆) | 300 | 400 |
(1)参加此次拓展活动的老师有 人,参加此次拓展活动的学生有 人;
(2)既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师,可知租用客车总数为 辆.
(3)你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
【题目】从甲地到乙地有![]() 三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
公交车用时的频数 公交车用时线路 |
|
|
|
| 合计 |
| 59 | 151 | 166 | 124 | 500 |
| 50 | 50 | 122 | 278 | 500 |
| 45 | 265 | 160 | 30 | 500 |
早高峰期间,乘坐_________(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大.
”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大.
【题目】超市为减小![]() 商品的积压,决定采取降价销售的策略,若某商品的原价为
商品的积压,决定采取降价销售的策略,若某商品的原价为![]() 元,随着不同幅度的降价,日销量(单位为件)发生相应的变化如表:
元,随着不同幅度的降价,日销量(单位为件)发生相应的变化如表:
降价(元) |
|
|
|
|
|
|
日销量(件) |
|
|
|
|
|
|
![]() 这个表反映了________ 和________ 两个变量之间的关系;
这个表反映了________ 和________ 两个变量之间的关系;
![]() 从表中可以看出每降价
从表中可以看出每降价![]() 元,日销量增加_ 件;
元,日销量增加_ 件;
![]() 可以估计降价之前的日销量为_ _件;
可以估计降价之前的日销量为_ _件;
![]() 设日销量为
设日销量为![]() 件,降价为
件,降价为![]() 元,由上表呈现的规律,猜想
元,由上表呈现的规律,猜想![]() 与
与![]() 的函数关系式为_
的函数关系式为_
![]() 当售价为
当售价为![]() 元时,日销量为 ________件.
元时,日销量为 ________件.