Question

【题目】已知E为平行四边形ABCD中AB边上一点，且BE=AB，连接DE交BC于F，交AC于G．
（1）求证：△BEF≌△CDF；
（2）试探究OF与AB有什么位置关系和数量关系，并说明理由．

Answer 1

【答案】
（1）证明：∵四边形ABCD是平行四边形，

∵AB∥CD，AB=CD，

∴∠E=∠CDF，∠EBF=∠DCF，

又∵BE=AB，

∴BE=DC，

在：△BEF和△CDF中，

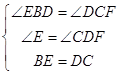
∴△BEF≌△CDF（AAS）；

（2）解：OF= AB，OF∥AB．理由如下：

∵OA=OC，BF=FC，

∴OF是△ABC的中位线．

∴OF= AB，OF∥AB．

【解析】（1）根据平行线的性质得出∠E=∠CDF，∠EBF=∠DCF，结合BE=CD=AB即可判断三角形的全等．（2）根据题意可判断出OF是△ABC的中位线，从而可判断出数量及位置关系．
【考点精析】根据题目的已知条件，利用平行四边形的性质的相关知识可以得到问题的答案，需要掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分．