题目内容
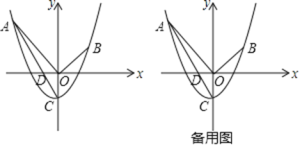
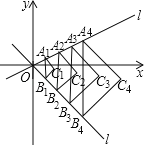
【题目】如图，在平面直角坐标系中，△A1B1C1，△A2B2C2，△A3B3C3，…，△AnBnCn均为等腰直角三角形，且∠C1＝∠C2＝∠C3＝…＝∠Cn＝90°，点A1，A2，A3，…，An和点B1，B2，B3，…，Bn分别在正比例函数y＝
x和y＝﹣x的图象上，且点A1，A2，A3，…，An的横坐标分别为1，2，3…n，线段A1B1，A2B2，A3B3，…，AnBn均与y轴平行．按照图中所反映的规律，则△AnBnCn的顶点Cn的坐标是____．（其中n为正整数）
【答案】（
，
）
【解析】
先求出A1（1，
），B1（1，-1），得出A1B1=-（-1）=
，根据等腰直角三角形的性质求出C1的坐标，再分别求出C2、C3、C4的坐标，得出规律，进而求出Cn的坐标；
解：∵x=1时，y=x=，y=-x=-1，
∴A1（1，），B1（1，-1）
∴A1B1=-（-1）=，
∵△A1B1C1为等腰直角三角形，
∴C1的横坐标是1+A1B1=
，
C1的纵坐标是-1+A1B1=
，
∴C1的坐标是（，）；
∵x=2时，y=x=1，y=-x=-2，
∴A2（2，1），B2（2，-2），
∴A2B2=1-（-2）=3，
∵△A2B2C2为等腰直角三角形，
∴C2的横坐标是2+A2B2=
，C2的纵坐标是-2+A2B2=-，
∴C2的坐标是（，-）；
同理，可得C3的坐标是（
，-
）；C4的坐标是（7，-1）；
…
∴△AnBnCn的顶点Cn的坐标是（
，-
）；
故答案为：（，-）；
【题目】某文具商店销售学习用品，已知某品牌钢笔的进价是20元，销售过程发现，每月销量y支与销售单价x元（x为正整数）之间满足一次函数关系，且每支钢笔的售价不低于进价，也不高于35元，下表是y与x之间的对应数据：
销售单价x（元） | … | 22 | 24 | 30 | … |
月销量y（只） | … | 92 | 84 | 60 | … |
（1）求y与x的函数关系式并直接写出自变量x的取值范围.
（2）每支钢笔的售价定为多少元时，月销售利润恰为600元？
（3）每支钢笔的售价定为多少元时可使月销售利润最大？最大的月利润是多少？
