题目内容
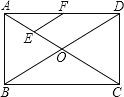
【题目】如图，在矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是AO、AD的中点，若AB=60cm，BC=80cm，则△AEF的周长是多少？
【答案】△AEF的周长是90cm．
【解析】试题分析：先根据勾股定理求出AC的长，由矩形的性质可知：矩形的两条对角线相等，可得BD=AC，即可得OD的长，在△AOD中，根据E、F分别是AO、AD在中点，分别求出AE、EF、AF的长，即可得△AEF的周长.
试题解析：在Rt△ABC中，AC=
=100cm，
在矩形ABCD中BD=AC=100cm， AD=BC=80cm，
∵ 点E、F分别是AO、AD的中点，
∴ EF是△AOD的中位线，
∴ EF=
OD=
BD=25，AF=
AD=
BC=40cm，AE=
AO=
AC=25，
∴ △AEF的周长=AE+AF+EF=90cm．
练习册系列答案
相关题目
【题目】在一次交通调查中，100辆汽车经过某地时车内人数如下：
乘车人数 | 1 | 2 | 3 | 4 | 5 |
车数 | x | 30 | y | 16 | 4 |
（1）x+y= ．
（2）若每辆车的平均人数为2.5，则中位数为 人．
（3）若每辆车的平均人数为2，则众数为 人．
（4）若x为30，则每辆车的平均人数为 人，中位数为 人．
