Question

【题目】如图，正六边形ABCDEF的边长为6cm，P是对角线BE上一动点，过点P作直线l与BE垂直，动点P从B点出发且以1cm/s的速度匀速平移至E点．设直线l扫过正六边形ABCDEF区域的面积为S（cm2），点P的运动时间为t（s），下列能反映S与t之间函数关系的大致图象是（　　）

A. B. C. D.

Answer 1

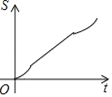
【答案】C

【解析】由题意得：BP=t，

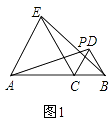
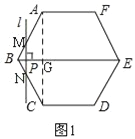
如图1，连接AC，交BE于G，Rt△ABG中，AB=6，∠ABG=60°，∴∠BAG=30°，

∴BG=AB=3，

由勾股定理得：AG= =3，∴AC=2AG=6，

当0≤t≤3时，PM=t，∴MN=2t，S=S△BMN=MNPB=× t2= t2，

所以选项A和B不正确；

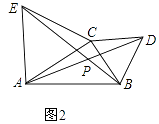
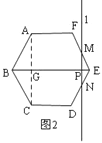
如图2，当9≤t≤12时，PE=12﹣t，

∵∠MEP=60°，∴tan∠MEP= ，∴PM=（12﹣t），∴MN=2PM=2（12﹣t），

∴S=S正六边形﹣S△EMN=2×（AF+BE）×AG﹣MNPE=（6+12）×3﹣×2（12﹣t）（12﹣t）=﹣t2+24t﹣90，

此二次函数的开口向下，

所以选项C正确，选项D不正确；

故选C．