题目内容
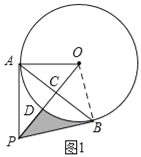
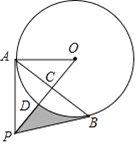
【题目】如图,点A在⊙O上,点P是⊙O外一点,PA切⊙O于点A,连接OP交⊙O于点D,作AB⊥OP于点C,交⊙O于点B,连接PB.
(1)求证:PB是⊙O的切线;
(2)若PC=9,AB=6![]() ,
,
①求图中阴影部分的面积;
②若点E是⊙O上一点,连接AE,BE,当AE=6![]() 时,BE= .
时,BE= .
【答案】(1)证明见解析;(2)①S阴影= 18![]() ﹣6π;②3
﹣6π;②3![]() ﹣3
﹣3![]() 或3
或3![]() +3
+3![]() .
.
【解析】试题分析:(1)由PA切⊙O于点A得:∠PAO=90°,再证明△APO≌△BPO,所以∠PBO=∠PAO=90°,可得结论;
(2)①先根据垂径定理得:BC=3![]() ,根据勾股定理求圆的半径OB的长,利用三角函数得:∠COB=60°,利用三角形的面积公式和扇形的面积公式分别求S△OPB和S扇形DOB的值,最后利用面积差得结论;
,根据勾股定理求圆的半径OB的长,利用三角函数得:∠COB=60°,利用三角形的面积公式和扇形的面积公式分别求S△OPB和S扇形DOB的值,最后利用面积差得结论;
②②分两种情况:
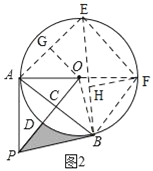
i)当点E在![]() 上时,如图2,作辅助线,构建直角三角形和等腰直角三角形,利用同弧所对的圆周角与半径及勾股定理分别计算EH和BH的长,相加即可得BE的长;
上时,如图2,作辅助线,构建直角三角形和等腰直角三角形,利用同弧所对的圆周角与半径及勾股定理分别计算EH和BH的长,相加即可得BE的长;
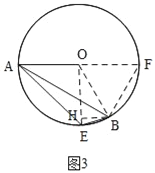
ii)当点E在劣弧![]() 上时,如图3,作辅助线,同理计算EH和BH的长,最后利用勾股定理求BE的长.
上时,如图3,作辅助线,同理计算EH和BH的长,最后利用勾股定理求BE的长.
试题解析:(1)如图1,连接OB,
∵OP⊥AB,OP经过圆心O,∴AC=BC,∴OP垂直平分AB,∴AP=BP,
∵OA=OB,OP=OP,∴△APO≌△BPO(SSS),∴∠PAO=∠PBO,
∵PA切⊙O于点A,∴AP⊥OA,∴∠PAO=90°,∴∠PBO=∠PAO=90°,∴OB⊥BP,
又∵点B在⊙O上,∴PB与⊙O相切于点B;
(2)①如图1,∵OP⊥AB,OP经过圆心O,∴BC=![]() AB=3
AB=3![]() ,
,
∵∠PBO=∠BCO=90°,∴∠PBC+∠OBC=∠OBC+∠BOC=90°,∴∠PBC=∠BOC,∴△PBC∽△BOC,
∴![]() ,∴OC=
,∴OC=![]() =
=![]() =3,
=3,
∴在Rt△OCB中,OB=![]() =
=![]() =6,tan∠COB=
=6,tan∠COB=![]() =
=![]() ,
,
∴∠COB=60°,
∴S△OPB=![]() ×OP×BC=
×OP×BC=![]() ×(3+9)×3
×(3+9)×3![]() =18
=18![]() ,S扇DOB=
,S扇DOB=![]() =6π,
=6π,
∴S阴影=S△OPB﹣S扇DOB=18![]() ﹣6π;
﹣6π;
②分两种情况:
i)当点E在![]() 上时,如图2,作直径AF,交⊙O于F,连接EF、EB,过O作OG⊥AE于G,过F作FH⊥EB于H,∴EG=AG=
上时,如图2,作直径AF,交⊙O于F,连接EF、EB,过O作OG⊥AE于G,过F作FH⊥EB于H,∴EG=AG=![]() AE=
AE=![]() ×6
×6![]() =3
=3![]() ,
,
∵∠AOB=120°,OA=OB,∴∠OAB=30°,∴∠BEF=∠OAB=30°,
Rt△OGE中,由①知:OA=6,∴OG=![]() =
=![]() =3
=3![]() ,∴AG=OG,
,∴AG=OG,
∴△OGA是等腰直角三角形,∴∠OAE=45°,∴∠EBF=∠OAE=45°,
∵AF是⊙O的直径,∴∠AEF=90°,∴△AEF是等腰直角三角形,∴EF=AE=6![]() ,
,
Rt△EHF中,∠BEF=30°,∴FH=![]() EF=3
EF=3![]() ,
,
∴EH=![]() =
=![]() =3
=3![]() ,
,
Rt△BHF中,∵∠EBF=45°,∴△BHF是等腰直角三角形,∴BH=FH=3![]() ,
,
∴BE=3![]() +3
+3![]() ,
,
ii)当点E在劣弧![]() 上时,如图3,
上时,如图3,
作直径AF,并⊙O于F,连接OB、OE、BF,过B作BH⊥OE于H,
∵AF为⊙O的直径,∴∠ABF=90°,
∵∠BAF=30°,∴∠F=∠BOF=60°,
∵OA=OE=6,AE=6![]() ,∴OA2+OE2=AE2,∴∠AOE=90°,∴∠EOF=90°,∴∠EOB=30°,
,∴OA2+OE2=AE2,∴∠AOE=90°,∴∠EOF=90°,∴∠EOB=30°,
Rt△OHB中,BH=![]() OB=3,∴OH=
OB=3,∴OH=![]() =3
=3![]() ,∴EH=6﹣3
,∴EH=6﹣3![]() ,
,
∴BE=![]() =
=![]() =3
=3![]() ﹣3
﹣3![]() ;
;
综上所述,BE的长为3![]() +3
+3![]() 或3
或3![]() ﹣3
﹣3![]() ;
;
故答案为:3![]() ﹣3
﹣3![]() 或3
或3![]() +3
+3![]() .
.