题目内容
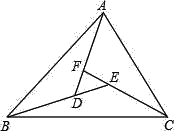
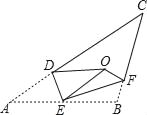
【题目】如图,∠BAD=∠CBE=∠ACF,∠FDE=64°,∠DEF=43°,求△ABC各内角的度数.
【答案】△ABC各内角的度数分别为64°、43°、73°.
【解析】
根据三角形外角性质得到∠FDE=∠BAD+∠ABD,而∠BAD=∠CBE,则∠FDE=∠BAD+∠CBE=∠ABC=64°;同理可得∠DEF=∠ACB=43°,然后根据三角形内角和定理计算∠BAC=180°﹣∠ABC﹣∠ACB即可.
∵∠FDE=∠BAD+∠ABD,∠BAD=∠CBE,∴∠FDE=∠BAD+∠CBE=∠ABC,∴∠ABC=64°;
同理:∠DEF=∠FCB+∠CBE=∠FCB+∠ACF=∠ACB,∴∠ACB=43°;
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣64°﹣43°=73°,∴△ABC各内角的度数分别为64°、43°、73°.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
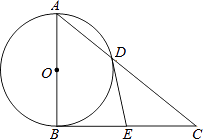
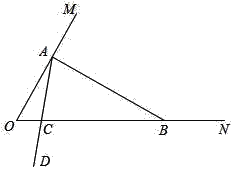
【题目】如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=100°,则∠C的度数为( )
A. 40° B. 41° C. 42° D. 43°
【题目】某中学数学活动小组为了调查居民的用水情况,从某社区的1500户家庭中随机抽取了30户家庭的月用水量,结果如下表所示:
月用水量(吨) | 3 | 4 | 5 | 7 | 8 | 9 | 10 |
户 数 | 4 | 3 | 5 | 11 | 4 | 2 | 1 |
(1)求这30户家庭月用水量的平均数,众数和中位数;
(2)根据上述数据,试估计该社区的月用水量;
(3)由于我国水资源缺乏,许多城市常利用分段计费的办法引导人们节约用水,即规定每个家庭的月基本用水量为m(吨),家庭月用水量不超过m(吨)的部分按原价收费,超过m吨部分加倍收费,你认为上述问题中的平均数、众数、中位数中哪一个量作为月基本用水量比较合理?简述理由。