题目内容
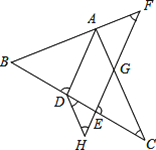
【题目】如图,在10×10的网格中,有一格点三角形ABC.(说明:顶点都在网格线交点处的三角形叫做格点三角形)

(1)将△ABC绕点C旋转180°,得到△A′B′C,请直接画出旋转后的△A′B′C.(友情提醒:别忘了标上相应的字母!)
(2)在网格中以AB为一边作格点△ABD(顶点在小正方形的顶点处的三角形称为格点三角形),使它的面积是△ABC的2倍,则点D的个数有个.
【答案】(1)见解析;(2)5
【解析】
(1)作出点A、B、C绕着点C旋转180°得到的对应点,再首尾顺次连接得到△ABC即可;
(2)先建立如图所示的坐标系,求出A,B,C三点的坐标,再求出直线AB的解析式,再求出过点CQ且与AB平行的直线方程,然后求得过点D的直线的方程并求出所过格点的个数.
解:(1)将△ABC绕点C旋转180°,得到△A′B′C即为所求的三角形,如图所示点C与点C重合

(2)建立如图所示的平面直角坐标系,则A(1,2),B(3,1),C(4,4),
设过直线AB的解析式为:y=kx+b,
∵A(2,1),B(3,1),
∴![]()
解得:
则设过C(4,4)与AB平行的直线的解析式为:y=![]() x+b1,
x+b1,
将x=4,y=4,代入得,4=![]() ×4+b1,解得,b1=6
×4+b1,解得,b1=6
∴b1-b=![]()
∵![]()
∴过点D且与AB平行的直线解析式为:![]()
∵在网格中以AB为一边作格点△ABD,∴点D的纵横坐标均为整数且大于等于0,小于等于10的整数,
∵当x为偶数时,y不是整数;∴x为奇数
∴当x=1时,y=![]() ×1+
×1+![]() =9,
=9,
当x=3时,y=![]() ×3+
×3+![]() =8,
=8,
当x=5时,y=![]() ×5+
×5+![]() =7,
=7,
当x=7时,y=![]() ×7+
×7+![]() =6,
=6,
当x=9时,y=![]() ×9+
×9+![]() =5,
=5,
所以,点D的坐标为:(1,9),(3,8),(5,7),(7,6),(9,5)
故在网格中以AB
5个

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案