题目内容
【题目】如图,已知点![]() 是双曲线
是双曲线![]() 在第一象限上的一动点,连接
在第一象限上的一动点,连接![]() ,以
,以![]() 为一边作等腰直角三角形
为一边作等腰直角三角形![]() (
(![]() ),点
),点![]() 在第四象限,随着点
在第四象限,随着点![]() 的运动,点
的运动,点![]() 的位置也不断的变化,但始终在某个函数图像上运动,则这个函数表达式为______.
的位置也不断的变化,但始终在某个函数图像上运动,则这个函数表达式为______.

【答案】![]() .
.
【解析】
设点B所在的反比例函数解析式为![]() ,分别过点A、B作AD⊥
,分别过点A、B作AD⊥![]() 轴于 D,BE⊥
轴于 D,BE⊥![]() 轴于点E,由全等三角形的判定定理可知△AOD
轴于点E,由全等三角形的判定定理可知△AOD![]() △OBE(ASA),故可得出
△OBE(ASA),故可得出![]() ,即可求得
,即可求得![]() 的值.
的值.
解:设点B所在的反比例函数解析式为![]() ,分别过点A、B作AD⊥
,分别过点A、B作AD⊥![]() 轴于 D,BE⊥
轴于 D,BE⊥![]() 轴于点E,如图:
轴于点E,如图:
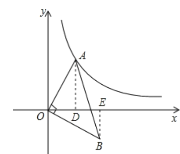
∵∠AOE+∠DOB=90°,∠AOE+∠OAD=90°,
∴∠OAD=∠BOE,
同理可得∠AOD=∠OBE,
在△AOD和△OBE中,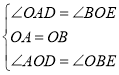 ,
,
∴△AOD![]() △OBE(ASA),
△OBE(ASA),
∵点B在第四象限,
∴![]() ,即
,即![]() ,
,
解得![]() ,
,
∴反比例函数的解析式为:![]() .
.
故答案为![]() .
.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
【题目】某工厂一周计划每日生产某产品100吨,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的吨数记为正数,减少的吨数记为负数)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减/吨 | ﹣1 | +3 | ﹣2 | +4 | +7 | ﹣5 | ﹣10 |
(1)生产量最多的一天比生产量最少的一天多生产多少吨?
(2)本周总生产量是多少吨?比原计划增加了还是减少了?增减数为多少吨?
(3)若本周总生产的产品全部由35辆货车一次性装载运输离开工厂,则平均每辆货车大约需装载多少吨?(结果精确到0.01吨)