题目内容
已知⊙O和⊙O′相切，它们的半径分别为3和4，则OO′=________．
1或7
分析：根据两圆相切，则两圆可能内切，也可能外切，
当两圆外切时，圆心距等于两圆半径之和；
当两圆内切时，圆心距等于两圆半径之差．
解答：根据题意，得：
当两圆外切时，则两个圆的圆心距d=4+3=7；
当两圆内切时，则两个圆的圆心距d=4-3=1．
∴圆心距OO′为7或1．
故答案为：1或7．
点评：本题考查了由两圆位置关系来判断半径和圆心距之间数量关系的方法．
分析：根据两圆相切，则两圆可能内切，也可能外切，
当两圆外切时，圆心距等于两圆半径之和；
当两圆内切时，圆心距等于两圆半径之差．
解答：根据题意，得：
当两圆外切时，则两个圆的圆心距d=4+3=7；
当两圆内切时，则两个圆的圆心距d=4-3=1．
∴圆心距OO′为7或1．
故答案为：1或7．
点评：本题考查了由两圆位置关系来判断半径和圆心距之间数量关系的方法．
练习册系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
已知⊙A和⊙B相切，两圆的圆心距为8cm，⊙A的半径为3cm，则⊙B的半径是（ ）
| A．5cm | B．3cm 或11cm | C．3cm | D．5cm或11cm |
已知⊙O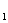
和⊙O
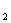相切，两圆的圆心距为9cm，⊙
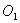的半径为4cm，则⊙O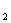的半径为（ ）
| A．5cm | B．13cm | C．9 cm 或13cm | D．5cm 或13cm |
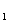和⊙O
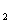相切，两圆的圆心距为9cm，⊙
的半径为4cm，则⊙O