题目内容
24、已知⊙A和⊙B相切，其半径分别为7和3，求以两圆圆心距为边长的正方形的面积？
分析：本题直接告诉了两圆的半径，根据数量关系与两圆位置关系的对应情况便可得到两圆圆心距，再根据正方形面积公式即可得出答案．
解答：解：根据题意，得
两圆外切时，P=7+3=10，
正方形的面积为10×10=100；
两圆内切时，P=R-r=4，
正方形的面积为4×4=16．
故正方形的面积为100或16．
两圆外切时，P=7+3=10，
正方形的面积为10×10=100；
两圆内切时，P=R-r=4，
正方形的面积为4×4=16．
故正方形的面积为100或16．
点评：本题考查了由数量关系来判断两圆位置关系的方法，特别注意相切的两种情况．
练习册系列答案
发散思维新课堂系列答案
相关题目
已知⊙A和⊙B相切，两圆的圆心距为8cm，⊙A的半径为3cm，则⊙B的半径是（ ）
| A．5cm | B．3cm 或11cm | C．3cm | D．5cm或11cm |
已知⊙O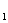
和⊙O
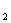相切，两圆的圆心距为9cm，⊙
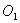的半径为4cm，则⊙O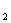的半径为（ ）
| A．5cm | B．13cm | C．9 cm 或13cm | D．5cm 或13cm |
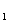和⊙O
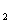相切，两圆的圆心距为9cm，⊙
的半径为4cm，则⊙O