题目内容
不能判定四边形ABCD是平行四边形的条件是( )
分析:平行四边形的五种判定方法分别是:
(1)两组对边分别平行的四边形是平行四边形;
(2)两组对边分别相等的四边形是平行四边形;
(3)一组对边平行且相等的四边形是平行四边形;
(4)两组对角分别相等的四边形是平行四边形;
(5)对角线互相平分的四边形是平行四边形.
根据平行四边形的判定逐一验证.
(1)两组对边分别平行的四边形是平行四边形;
(2)两组对边分别相等的四边形是平行四边形;
(3)一组对边平行且相等的四边形是平行四边形;
(4)两组对角分别相等的四边形是平行四边形;
(5)对角线互相平分的四边形是平行四边形.
根据平行四边形的判定逐一验证.
解答: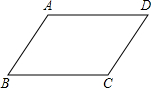 解:A、“∠A=∠C,∠B=∠D”是四边形ABCD的两组对角相等,可以判定四边形ABCD是平行四边形;故本选项正确;
解:A、“∠A=∠C,∠B=∠D”是四边形ABCD的两组对角相等,可以判定四边形ABCD是平行四边形;故本选项正确;
B、“AB∥CD,AD=BC”是四边形ABCD的一组对边平行,另一组对边相等,不可以判定四边形ABCD是平行四边形;故本选项错误;
C、∵AB∥CD,
∴∠B+∠C=180°.
又∵∠A=∠C,
∴∠A+∠B=180°,
∴AD∥BC,
∴四边形ABCD是平行四边形;故本选项正确;
D、“AB∥CD,AB=CD”是四边形ABCD的一组对边平行且相等,可以判定四边形ABCD是平行四边形;故本选项正确.
故选B.
 解:A、“∠A=∠C,∠B=∠D”是四边形ABCD的两组对角相等,可以判定四边形ABCD是平行四边形;故本选项正确;
解:A、“∠A=∠C,∠B=∠D”是四边形ABCD的两组对角相等,可以判定四边形ABCD是平行四边形;故本选项正确;B、“AB∥CD,AD=BC”是四边形ABCD的一组对边平行,另一组对边相等,不可以判定四边形ABCD是平行四边形;故本选项错误;
C、∵AB∥CD,
∴∠B+∠C=180°.
又∵∠A=∠C,
∴∠A+∠B=180°,
∴AD∥BC,
∴四边形ABCD是平行四边形;故本选项正确;
D、“AB∥CD,AB=CD”是四边形ABCD的一组对边平行且相等,可以判定四边形ABCD是平行四边形;故本选项正确.
故选B.
点评:本题考查平行四边形的判定,需注意“一组对边平行,另一组对边相等”的四边形不一定是平行四边形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
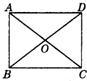 6、如图,下列条件不能判定四边形ABCD是矩形的是( )
6、如图,下列条件不能判定四边形ABCD是矩形的是( )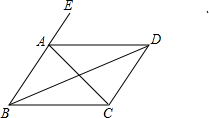 如图,四边形ABCD中,AC、BD是对角线,点E在BA的延长线上,下列条件不能判定
如图,四边形ABCD中,AC、BD是对角线,点E在BA的延长线上,下列条件不能判定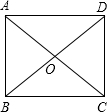 如图,下列条件不能判定四边形ABCD是矩形的是
如图,下列条件不能判定四边形ABCD是矩形的是