Ő‚ńŅńŕ»›
£®2013•—Ó∆÷«Ý∂Ģń££©»ÁÕľ1£¨“—÷™°—OĶńįŽĺ∂≥§ő™3£¨Ķ„A «°—O…Ō“Ľ∂®Ķ„£¨Ķ„Pő™°—O…Ō≤ĽÕ¨”ŕĶ„AĶń∂ĮĶ„£ģ
£®1£©ĶĪtanA=
Ī£¨«ůAPĶń≥§£Ľ
£®2£©»ÁĻŻ°—QĻżĶ„P°ĘO£¨«“Ķ„Q‘ŕ÷ĪŌŖAP…Ō£®»ÁÕľ2£©£¨…ŤAP=x£¨QP=y£¨«ůyĻō”ŕxĶńļĮ żĻōŌĶ Ĺ£¨≤Ę–ī≥ŲļĮ żĶń∂®“Ś”Ú£Ľ
£®3£©‘ŕ£®2£©ĶńŐűľĢŌ¬£¨ĶĪtanA=
Ī£®»ÁÕľ3£©£¨īś‘ŕ°—M”Ž°—OŌŗńŕ«–£¨Õ¨ Ī”Ž°—QŌŗÕ‚«–£¨«“OM°ÕOQ£¨ ‘«ů°—MĶńįŽĺ∂Ķń≥§£ģ

£®1£©ĶĪtanA=
| 1 |
| 2 |
£®2£©»ÁĻŻ°—QĻżĶ„P°ĘO£¨«“Ķ„Q‘ŕ÷ĪŌŖAP…Ō£®»ÁÕľ2£©£¨…ŤAP=x£¨QP=y£¨«ůyĻō”ŕxĶńļĮ żĻōŌĶ Ĺ£¨≤Ę–ī≥ŲļĮ żĶń∂®“Ś”Ú£Ľ
£®3£©‘ŕ£®2£©ĶńŐűľĢŌ¬£¨ĶĪtanA=
| 4 |
| 3 |

∑÷őŲ£ļ£®1£©ĻżĶ„P◊ųPB°ÕOAĹĽAOĶń—”≥§ŌŖ”ŕB£¨Ń¨Ĺ”OP£¨…ŤPB=a£¨łýĺ›°ŌAĶń’ż«–÷ĶĪŪ ĺ≥ŲAB=2a£¨‘ŔĪŪ ĺ≥ŲOE=2a-3£¨‘ŕRt°ųPOB÷–£¨ņŻ”√ĻīĻ…∂®ņŪŃ–∑Ĺ≥Ő«ů≥Ųa£¨»Ľļů‘ŕRt°ųABP÷–£¨ņŻ”√ĻīĻ…∂®ņŪŃ– Ĺľ∆ň„ľīŅ…«ů≥ŲAP£Ľ
£®2£©Ń¨Ĺ”OP°ĘOQ£¨łýĺ›Ķ»ĪŖ∂‘Ķ»Ĺ«Ņ…Ķ√°ŌP=°ŌPOQ=°ŌA£¨«ů≥Ų°ųAOPļÕ°ųPQOŌŗň∆£¨ņŻ”√Ōŗň∆»żĹ«–ő∂‘”¶ĪŖ≥…Ī»ņżŃ– Ĺ’ŻņŪľīŅ…Ķ√ĶĹy”ŽxĶńĻōŌĶ Ĺ£¨łýĺ›÷Īĺ∂ «‘≤Ķń◊Ó≥§ĶńŌ“–ī≥ŲxĶń»°÷Ķ∑∂őߣĽ
£®3£©ĻżĶ„O◊ųOC°ÕAP”ŕC£¨łýĺ›°ŌAĶń’ż«–÷Ķ£¨…ŤOC=4b£¨‘ÚAC=3b£¨‘ŕRt°ųAOC÷–£¨ņŻ”√ĻīĻ…∂®ņŪŃ–∑Ĺ≥Ő«ů≥Ųb£¨ī”∂ÝĶ√ĶĹOC°ĘAC£¨‘Ŕłýĺ›Ķ»—Ł»żĹ«–ő»żŌŖļŌ“ĽĶń–‘÷ Ņ…Ķ√PC=AC£¨…Ť°—QĶńįŽĺ∂ő™c£¨»ĽļůĪŪ ĺ≥ŲCQ£¨‘ŕRt°ųCOQ÷–£¨ņŻ”√ĻīĻ…∂®ņŪŃ–∑Ĺ≥Ő«ů≥Ųc£¨…Ť°—MĶńįŽĺ∂ő™r£¨łý囑≤”Ž‘≤ĶńőĽ÷√ĻōŌĶĪŪ ĺ≥ŲMQ°ĘMO»ĽļůņŻ”√ĻīĻ…∂®ņŪŃ–∑Ĺ≥Ő«ůĹ‚ľīŅ…Ķ√ĶĹrĶń÷Ķ£¨ī”∂ÝĶ√Ĺ‚£ģ
£®2£©Ń¨Ĺ”OP°ĘOQ£¨łýĺ›Ķ»ĪŖ∂‘Ķ»Ĺ«Ņ…Ķ√°ŌP=°ŌPOQ=°ŌA£¨«ů≥Ų°ųAOPļÕ°ųPQOŌŗň∆£¨ņŻ”√Ōŗň∆»żĹ«–ő∂‘”¶ĪŖ≥…Ī»ņżŃ– Ĺ’ŻņŪľīŅ…Ķ√ĶĹy”ŽxĶńĻōŌĶ Ĺ£¨łýĺ›÷Īĺ∂ «‘≤Ķń◊Ó≥§ĶńŌ“–ī≥ŲxĶń»°÷Ķ∑∂őߣĽ
£®3£©ĻżĶ„O◊ųOC°ÕAP”ŕC£¨łýĺ›°ŌAĶń’ż«–÷Ķ£¨…ŤOC=4b£¨‘ÚAC=3b£¨‘ŕRt°ųAOC÷–£¨ņŻ”√ĻīĻ…∂®ņŪŃ–∑Ĺ≥Ő«ů≥Ųb£¨ī”∂ÝĶ√ĶĹOC°ĘAC£¨‘Ŕłýĺ›Ķ»—Ł»żĹ«–ő»żŌŖļŌ“ĽĶń–‘÷ Ņ…Ķ√PC=AC£¨…Ť°—QĶńįŽĺ∂ő™c£¨»ĽļůĪŪ ĺ≥ŲCQ£¨‘ŕRt°ųCOQ÷–£¨ņŻ”√ĻīĻ…∂®ņŪŃ–∑Ĺ≥Ő«ů≥Ųc£¨…Ť°—MĶńįŽĺ∂ő™r£¨łý囑≤”Ž‘≤ĶńőĽ÷√ĻōŌĶĪŪ ĺ≥ŲMQ°ĘMO»ĽļůņŻ”√ĻīĻ…∂®ņŪŃ–∑Ĺ≥Ő«ůĹ‚ľīŅ…Ķ√ĶĹrĶń÷Ķ£¨ī”∂ÝĶ√Ĺ‚£ģ
Ĺ‚īū£ļĹ‚£ļ£®1£©»ÁÕľ1£¨ĻżĶ„P◊ųPB°ÕOAĹĽAOĶń—”≥§ŌŖ”ŕB£¨Ń¨Ĺ”OP£¨…ŤPB=a£¨
°ŖtanA=
£¨
°ŗAB=2a£¨
°ŗOB=AB-OA=2a-3£¨
‘ŕRt°ųPOB÷–£¨PB2+OB2=OP2£¨
ľīa2+£®2a-3£©2=32£¨
Ĺ‚Ķ√a1=
£¨a2=0£®…Š»•£©£¨
°ŗAB=2°Ń
=
£¨
‘ŕRt°ųABP÷–£¨AP=
=
=
£Ľ
£®2£©Ń¨Ĺ”OP°ĘOQ£¨‘ÚAO=PO£¨PQ=OQ£¨
°ŗ°ŌP=°ŌA£¨°ŌPOQ=°ŌP£¨
°ŗ°ŌP=°ŌPOQ=°ŌA£¨
°ŗ°ųAOP°◊°ųPQO£¨
°ŗ
=
£¨
ľī
=
£¨
’ŻņŪĶ√£¨y=
£¨
°Ŗ°—OĶńįŽĺ∂ő™3£¨Ķ„P≤ĽÕ¨”ŕĶ„A£¨
°ŗ0£ľx°‹6£Ľ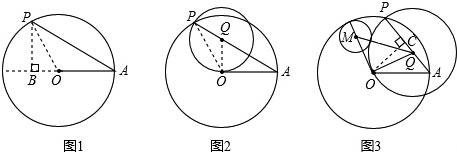
°ŗy=
£®0£ľx°‹6£©£Ľ
£®3£©ĻżĶ„O◊ųOC°ÕAP”ŕC£¨
°ŖtanA=
£¨
°ŗ…ŤOC=4b£¨AC=3b£¨
‘ŕRt°ųAOC÷–£¨OC2+AC2=OA2£¨
ľī£®4b£©2+£®3b£©2=32£¨
Ĺ‚Ķ√b=
£¨
°ŗOC=4°Ń
=
£¨AC=3°Ń
=
£¨
łýĺ›īĻĺ∂∂®ņŪ£¨PC=AC=
£¨
…Ť°—QĶńįŽĺ∂ő™c£¨‘ÚCQ=QP-PC=c-
£¨
‘ŕRt°ųCOQ÷–£¨OC2+CQ2=OQ2£¨
ľī£®
£©2+£®c-
£©2=c2£¨
Ĺ‚Ķ√c=
£¨
…Ť°—MĶńįŽĺ∂ő™r£¨
°Ŗ°—M”Ž°—OŌŗńŕ«–£¨Õ¨ Ī”Ž°—QŌŗÕ‚«–£¨
°ŗMO=3-r£¨MQ=r+
£¨
‘ŕRt°ųOMQ÷–£¨MO2+OQ2=MQ2£¨
ľī£®3-r£©2+£®
£©2=£®r+
£©2£¨
Ĺ‚Ķ√r=
£ģ
°ŖtanA=
| 1 |
| 2 |
°ŗAB=2a£¨
°ŗOB=AB-OA=2a-3£¨
‘ŕRt°ųPOB÷–£¨PB2+OB2=OP2£¨
ľīa2+£®2a-3£©2=32£¨
Ĺ‚Ķ√a1=
| 12 |
| 5 |
°ŗAB=2°Ń
| 12 |
| 5 |
| 24 |
| 5 |
‘ŕRt°ųABP÷–£¨AP=
| PB2+AB2 |
(
|
12
| ||
| 5 |
£®2£©Ń¨Ĺ”OP°ĘOQ£¨‘ÚAO=PO£¨PQ=OQ£¨
°ŗ°ŌP=°ŌA£¨°ŌPOQ=°ŌP£¨
°ŗ°ŌP=°ŌPOQ=°ŌA£¨
°ŗ°ųAOP°◊°ųPQO£¨
°ŗ
| QP |
| OP |
| OP |
| AP |
ľī
| y |
| 3 |
| 3 |
| x |
’ŻņŪĶ√£¨y=
| 9 |
| x |
°Ŗ°—OĶńįŽĺ∂ő™3£¨Ķ„P≤ĽÕ¨”ŕĶ„A£¨
°ŗ0£ľx°‹6£Ľ

°ŗy=
| 9 |
| x |
£®3£©ĻżĶ„O◊ųOC°ÕAP”ŕC£¨
°ŖtanA=
| 4 |
| 3 |
°ŗ…ŤOC=4b£¨AC=3b£¨
‘ŕRt°ųAOC÷–£¨OC2+AC2=OA2£¨
ľī£®4b£©2+£®3b£©2=32£¨
Ĺ‚Ķ√b=
| 3 |
| 5 |
°ŗOC=4°Ń
| 3 |
| 5 |
| 12 |
| 5 |
| 3 |
| 5 |
| 9 |
| 5 |
łýĺ›īĻĺ∂∂®ņŪ£¨PC=AC=
| 9 |
| 5 |
…Ť°—QĶńįŽĺ∂ő™c£¨‘ÚCQ=QP-PC=c-
| 9 |
| 5 |
‘ŕRt°ųCOQ÷–£¨OC2+CQ2=OQ2£¨
ľī£®
| 12 |
| 5 |
| 9 |
| 5 |
Ĺ‚Ķ√c=
| 5 |
| 2 |
…Ť°—MĶńįŽĺ∂ő™r£¨
°Ŗ°—M”Ž°—OŌŗńŕ«–£¨Õ¨ Ī”Ž°—QŌŗÕ‚«–£¨
°ŗMO=3-r£¨MQ=r+
| 5 |
| 2 |
‘ŕRt°ųOMQ÷–£¨MO2+OQ2=MQ2£¨
ľī£®3-r£©2+£®
| 5 |
| 2 |
| 5 |
| 2 |
Ĺ‚Ķ√r=
| 9 |
| 11 |
Ķ„∆ņ£ļĪĺŐ‚Ņľ≤ťŃň‘≤Ķń◊ŘļŌŐ‚–Õ£¨÷ų“™ņŻ”√ŃňĹ‚÷ĪĹ«»żĹ«–ő£¨ĻīĻ…∂®ņŪ£¨Õ¨“ĽłŲ‘≤ĶńįŽĺ∂ŌŗĶ»£¨Ķ»ĪŖ∂‘Ķ»Ĺ«Ķń–‘÷ £¨Ōŗň∆»żĹ«–őĶńŇ–∂®”Ž–‘÷ £¨‘≤”Ž‘≤ĶńőĽ÷√ĻōŌĶ£¨◊ųł®÷ķŌŖĻĻ‘ž≥Ų÷ĪĹ«»żĹ«–ő”ŽŌŗň∆»żĹ«–ő «Ĺ‚Ő‚ĶńĻōľŁ£¨ń—Ķ„‘ŕ”ŕ∑īłīņŻ”√ĻīĻ…∂®ņŪŃ–≥Ų∑Ĺ≥Ő«ůĹ‚£ģ

Ń∑Ōį≤ŠŌĶŃ–īūįł
ŌŗĻōŐ‚ńŅ
 £®2013•—Ó∆÷«Ý∂Ģń££©Ĺę÷ĪĹ«◊ÝĪÍŌĶ÷–“ĽīőļĮ żĶńÕľŌů”Ž◊ÝĪÍ÷Šőß≥…Ķń»żĹ«–ő£¨Ĺ–◊Ųīň“ĽīőļĮ żĶń◊ÝĪÍ»żĹ«–ő£ģņż»Á£¨Õľ÷–Ķń“ĽīőļĮ żÕľŌů”Žx°Ęy÷Š∑÷ĪūĹĽ”ŕĶ„A°ĘB£¨‘Ú°ųABOő™īň“ĽīőļĮ żĶń◊ÝĪÍ»żĹ«–ő£¨“ĽīőļĮ ż
£®2013•—Ó∆÷«Ý∂Ģń££©Ĺę÷ĪĹ«◊ÝĪÍŌĶ÷–“ĽīőļĮ żĶńÕľŌů”Ž◊ÝĪÍ÷Šőß≥…Ķń»żĹ«–ő£¨Ĺ–◊Ųīň“ĽīőļĮ żĶń◊ÝĪÍ»żĹ«–ő£ģņż»Á£¨Õľ÷–Ķń“ĽīőļĮ żÕľŌů”Žx°Ęy÷Š∑÷ĪūĹĽ”ŕĶ„A°ĘB£¨‘Ú°ųABOő™īň“ĽīőļĮ żĶń◊ÝĪÍ»żĹ«–ő£¨“ĽīőļĮ ż