题目内容
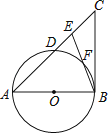
【题目】如图,平行四边形ABCD中,AB⊥AC,AB=1,BC= ![]() .对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F. 
(1)证明:当旋转角为90°时,四边形ABEF是平行四边形;
(2)试说明在旋转过程中,线段AF与EC总保持相等;
(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时AC绕点O顺时针旋转的度数.
【答案】
(1)证明:当∠AOF=90°时,
∵∠BAO=∠AOF=90°,
∴AB∥EF,
又∵AF∥BE,
∴四边形ABEF为平行四边形
(2)证明:∵四边形ABCD为平行四边形,
在△AOF和△COE中
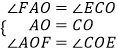 .
.
∴△AOF≌△COE(ASA).
∴AF=EC
(3)解:四边形BEDF可以是菱形.
理由:如图,连接BF,DE
由(2)知△AOF≌△COE,得OE=OF,
∴EF与BD互相平分.
∴当EF⊥BD时,四边形BEDF为菱形.
在Rt△ABC中,AC= ![]() =
= ![]() =2,
=2,
∴OA=1=AB,
又∵AB⊥AC,
∴∠AOB=45°,
∴∠AOF=45°,
∴AC绕点O顺时针旋转45°时,四边形BEDF为菱形.
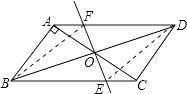
【解析】(1)当旋转角为90°时,∠AOF=90°,由AB⊥AC,可得AB∥EF,即可证明四边形ABEF为平行四边形;(2)证明△AOF≌△COE即可;(3)EF⊥BD时,四边形BEDF为菱形,可根据勾股定理求得AC=2,∴OA=1=AB,又AB⊥AC,∴∠AOB=45°.
【考点精析】根据题目的已知条件,利用平行四边形的判定与性质和菱形的判定方法的相关知识可以得到问题的答案,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.