题目内容
【题目】综合与探究
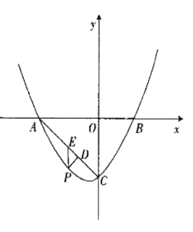
如图,在平面直角坐标系中,点![]() 的坐标分别为
的坐标分别为![]() ,点
,点![]() 在
在![]() 轴上,其坐标为
轴上,其坐标为![]() ,抛物线经过点
,抛物线经过点![]() 为第三象限内抛物线上一动点.
为第三象限内抛物线上一动点.
![]() 求该抛物线的解析式.
求该抛物线的解析式.
![]() 连接
连接![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,当
,当![]() 的周长最大时,求
的周长最大时,求![]() 点的坐标和
点的坐标和![]() 周长的最大值.
周长的最大值.
![]() 若点
若点![]() 为
为![]() 轴上一动点,点
轴上一动点,点![]() 为平面直角坐标系内一点.当点
为平面直角坐标系内一点.当点![]() 构成菱形时,请直接写出点
构成菱形时,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)P(2,
;(2)P(2,![]() )
)![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
⑴ 代入A、B点坐标得出抛物线的交点式y=a(x+4)(x-2),然后代入C点坐标即可求出;
⑵ 首先根据勾股定理可以求出AC=5,通过PE∥y轴,得到△PED∽△AOC,PD:AO=DE:OC=PE:AC,得到PD:4=DE:3=PE:5,PD,DE分别用PE表示,可得△PDE的周长=![]() PE,要使△PDE周长最大,PE取最大值即可;设P点的横坐标a,那么纵坐标为
PE,要使△PDE周长最大,PE取最大值即可;设P点的横坐标a,那么纵坐标为![]() a2+
a2+![]() a-3,根据E点在AC所在的直线上,求出解析式,那么E点的横坐标a,纵坐标-
a-3,根据E点在AC所在的直线上,求出解析式,那么E点的横坐标a,纵坐标-![]() a-3,从而求出PE含a的二次函数式,求出PE最大值,进而求出P点坐标及△PDE周长.
a-3,从而求出PE含a的二次函数式,求出PE最大值,进而求出P点坐标及△PDE周长.
⑶ 分类讨论
① 当BM为对角线时点F在y轴上,根据对称性得到点F的坐标.
② 当BM为边时,BC也为边时,求出BC长直接可以写出F点坐标,分别是点M在![]() 轴负半轴上时,点F的坐标为
轴负半轴上时,点F的坐标为![]() ;点M在
;点M在![]() 轴正半轴上时,点F的坐标为
轴正半轴上时,点F的坐标为![]() .
.
③ 当BM为边时,BC也为对角线时,首先求出BC所在直线的解析式![]()
,然后求出BC中点的坐标![]() ,MF所在直线也经过这点并且与BC所在的直线垂直,所以可以求出MF所在直线的解析式
,MF所在直线也经过这点并且与BC所在的直线垂直,所以可以求出MF所在直线的解析式![]() ,可以求出M点坐标
,可以求出M点坐标![]() ,求出F点的横坐标
,求出F点的横坐标![]() ,代入MF解析式求出纵坐标
,代入MF解析式求出纵坐标![]() ,得到F
,得到F![]()
解:![]() 抛物线经过点
抛物线经过点![]() ,它们的坐标分别为
,它们的坐标分别为![]() ,
,
故设其解析式为![]() .
.
又![]() 抛物线经过点
抛物线经过点![]() ,代入解得
,代入解得![]() ,
,
则抛物线的解析式为![]() .
.
![]()
![]() ,
,
![]() .
.
![]() .
.
又![]() 轴,
轴,![]() ,
,
∴△PDE∽△AOC.
![]() ,即
,即![]() ,
,
![]()
∴![]() 的周长
的周长![]()
则要使![]() 周长最大,
周长最大,![]() 取最大值即可.
取最大值即可.
易得![]() 所在直线的解析式为
所在直线的解析式为![]() .
.
设点![]() ,
,
则![]() ,
,
当![]() 时,取得最
时,取得最![]() 大值,最大值为
大值,最大值为![]() ,则
,则![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]()
提示:具体分情况进行讨论,如图.
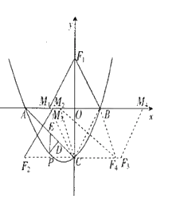
① ![]() 为对角线时,显然,点
为对角线时,显然,点![]() 在
在![]() 轴上,根据对称性得到点
轴上,根据对称性得到点![]() 的坐标为
的坐标为![]() ;
;
②当![]() 为边时,
为边时,![]() ,则有以下几种情况:
,则有以下几种情况:
(I)![]() 为边时,
为边时,
点![]() 在
在![]() 轴负半轴上时,点
轴负半轴上时,点![]() 的坐标为
的坐标为![]() ;
;
点![]() 在
在![]() 轴正半轴上时,点
轴正半轴上时,点![]() 的坐标为
的坐标为![]() .
.
(I) ![]() 为对角线时,
为对角线时,
根据点![]() ,点
,点![]() 可得
可得![]() 所在直线的解析式为
所在直线的解析式为![]()
![]() 中点的坐标为
中点的坐标为![]()
则MF所在的直线过线段![]() 的中点,并垂直于
的中点,并垂直于![]() ,得到其解析式为
,得到其解析式为![]() .
.
交![]() 轴于
轴于![]() 点,则点
点,则点![]() 的横坐标为
的横坐标为![]() ,代入
,代入![]() 的解析式得到
的解析式得到![]() ,
,
故点![]() 的坐标为
的坐标为![]() ,
,
综上所述,点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]()

 阅读快车系列答案
阅读快车系列答案【题目】万州三中初中数学组深知人生最具好奇心和幻想力、创造力的时期是中学时代,经研究,为我校每一个初中生推荐一本中学生素质数育必读书《数学的奥秘》,这本书就是专门为好奇的中学生准备的.这本书不但给于我们知识,解答生活中的疑惑,更重要的是培养我们细致观察、认真思考、勤于动手的能力.经过一学期的阅读和学习,为了了解学生阅读效果,我们从初一、初二的学生中随机各选20名,对《数学的奥秘》此书阅读效果做测试(此次测试满分:100分).通过测试,我们收集到20名学生得分的数据如下:
初一 | 96 | 100 | 89 | 95 | 62 | 75 | 93 | 86 | 86 | 93 |
95 | 95 | 88 | 94 | 95 | 68 | 92 | 80 | 78 | 90 | |
初二 | 100 | 98 | 96 | 95 | 94 | 92 | 92 | 92 | 92 | 92 |
86 | 84 | 83 | 82 | 78 | 78 | 74 | 64 | 60 | 92 |
通过整理,两组数据的平均数、中位数、众数和方差如表:
年级 | 平均数 | 中位数 | 众数 | 方差 |
初一 | 87.5 | 91 | m | 96.15 |
初二 | 86.2 | n | 92 | 113.06 |
某同学将初一学生得分按分数段(![]() ,
,![]() ,
,![]() ,
,![]() ),绘制成频数分布直方图,初二同学得分绘制成扇形统计图,如图(均不完整),初一学生得分频数分布直方图 初二学生得分扇形统计图(注:x表示学生分数)
),绘制成频数分布直方图,初二同学得分绘制成扇形统计图,如图(均不完整),初一学生得分频数分布直方图 初二学生得分扇形统计图(注:x表示学生分数)
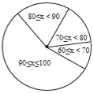
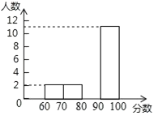
请完成下列问题:
(1)初一学生得分的众数![]() ________;初二学生得分的中位数
________;初二学生得分的中位数![]() ________;
________;
(2)补全频数分布直方图;扇形统计图中,![]() 所对用的圆心角为________度;
所对用的圆心角为________度;
(3)经过分析________学生得分相对稳定(填“初一”或“初二”);
(4)你认为哪个年级阅读效果更好,请说明理由.