Question

【题目】（1）叙述三角形中位线定理,并运用平行四边形的知识证明；

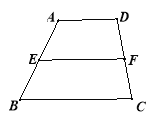
（2）运用三角形中位线的知识解决如下问题：如图，在四边形ABCD中，AD∥BC,E,F分别是AB,CD的中点，求证EF=.

Answer 1

【答案】（1）、三角形的中位线平行且等于第三边的一半，证明过程见解析；（2）、证明过程见解析

【解析】

试题分析：（1）、过点C作 CE∥AB交DE 的延长线于点F，可证四边形ADCF是平行四边形，从而得出答案；（2）、连接AF,并延长交BC的延长线于点G,证△ADF≌△GCF,则AF=CG,AD=CG，得出答案.

试题解析：（1）、定理：三角形的中位线平行且等于第三边的一半.

已知，D,E是△ABC的边AB,AC的中点，求证DE=且DE∥BC.

过点C作 CE∥AB交DE 的延长线于点F，可证四边形ADCF是平行四边形，

四边形BDFC是平行四边形， ∴DE=且DE∥BC

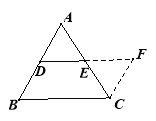
（2）、连接AF,并延长交BC的延长线于点G,证△ADF≌△GCF,则AF=CG,AD=CG

由（1）的结论可证.