题目内容
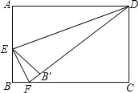
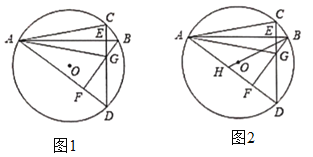
【题目】已知![]() 是圆
是圆![]() 的两条弦,
的两条弦,![]() 于
于![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.
(1)如图1,连接![]() ,求证:
,求证:![]() ;
;
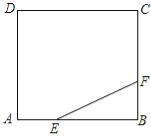
(2)如图2,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,若
,若![]() 平分
平分![]() ,求圆
,求圆![]() 的半径和
的半径和![]() 的长.
的长.
【答案】(1)见解析;(2)圆O的半径2.5;![]()
【解析】
(1)连接BC,如图,根据已知条件易得∠D=∠ABG,进而利用全等三角形的判定定理证明△BCE≌△BGE,接下来根据全等三角形的性质,利用线段垂直平分线的性质即可证得结论;
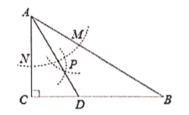
(2)连接CO并延长交⊙O于M,连接AM,可得![]() ,由已知AG=4,可得AM、AC的值,根据勾股定理求出CM,即可得圆O的半径;过点H作HN⊥AB,过点O作OP⊥AB,如图,联系三角函数的知识、角平分线的性质及勾股定理进行推理,即可求出AH的长.
,由已知AG=4,可得AM、AC的值,根据勾股定理求出CM,即可得圆O的半径;过点H作HN⊥AB,过点O作OP⊥AB,如图,联系三角函数的知识、角平分线的性质及勾股定理进行推理,即可求出AH的长.
连接![]() ,
,

![]() ,
,
![]() ,
,
![]() .
.
![]() 弧
弧![]() 弧
弧![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)如图,连接![]() 并延长交
并延长交![]() 于
于![]() ,连接
,连接![]() ,
,

![]() 是圆
是圆![]() 的直径,
的直径,
![]() .
.
![]() 弧
弧![]() 弧
弧![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() 圆
圆![]() 的半径为
的半径为![]() ,
,
过![]() 作
作![]() 于
于![]() ,可得
,可得![]() ,
,
![]() .
.
在![]() 中,
中,![]() ,
,
设![]() ,则
,则![]() ,
,
![]() 平分
平分![]()
![]() .
.
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() 在
在![]() 中,
中,![]() ,
,
过![]() 作
作![]() 于
于![]() ,则
,则![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
故答案为:(1)见解析;(2)圆O的半径2.5;![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目