题目内容
如图,一次函数 的图象与反比例函数
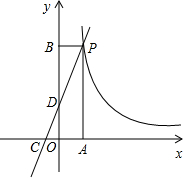
的图象与反比例函数 的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交
的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交 轴、
轴、 轴于点C、D,且S△PBD=4,
轴于点C、D,且S△PBD=4, .
.

小题1:求点D的坐标;
小题2:求一次函数与反比例函数的解析式;
小题3:根据图象写出当 时,一次函数的值大于反比例
时,一次函数的值大于反比例
函数的值的 的取值范围.
的取值范围.
 的图象与反比例函数
的图象与反比例函数 的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交
的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交 轴、
轴、 轴于点C、D,且S△PBD=4,
轴于点C、D,且S△PBD=4, .
.
小题1:求点D的坐标;
小题2:求一次函数与反比例函数的解析式;
小题3:根据图象写出当
 时,一次函数的值大于反比例
时,一次函数的值大于反比例函数的值的
 的取值范围.
的取值范围.小题1:D(0,2)
小题2:
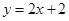
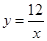
小题3:
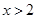
(1)把x=0代入y=kx+2即可求出D的坐标;根据相似三角形的判定得出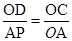 ,求出AP,即可求出BD;
,求出AP,即可求出BD;
(2)根据三角形PBD的面积求出P的坐标,把P的坐标分别代入一次函数和反比例函数的解析式求出即可;
(3)根据图象上P的坐标求出即可;
解:(1)在y=kx+2中,当x=0,得:y=2,
∴点D的坐标是(0,2),
∵AP∥OD,
∴△PAC∽△DOC,
∵ =
=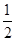 ,
,
∴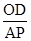 =
= =
=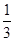 ,
,
∴AP=6,
∵BD=6-2=4,
答:点D的坐标是(0,2),BD的长是4.
(2)∵S△PBD=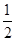 PB?BD=
PB?BD=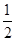 ×PB×4=4,
×PB×4=4,
∴BP=2,
∴P(2,6),
把P(2,6)分别代入y=kx+2和y=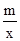 得:k=2,m=12,
得:k=2,m=12,
∴一次函数的解析式是y=2x+2,反比例函数的解析式是y=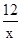 ,
,
(3)由图形可知一次函数的值大于反比例函数值的x的取值范围是x>2.
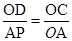 ,求出AP,即可求出BD;
,求出AP,即可求出BD;(2)根据三角形PBD的面积求出P的坐标,把P的坐标分别代入一次函数和反比例函数的解析式求出即可;
(3)根据图象上P的坐标求出即可;
解:(1)在y=kx+2中,当x=0,得:y=2,
∴点D的坐标是(0,2),
∵AP∥OD,
∴△PAC∽△DOC,
∵
 =
=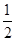 ,
,∴
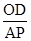 =
= =
=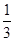 ,
,∴AP=6,
∵BD=6-2=4,
答:点D的坐标是(0,2),BD的长是4.
(2)∵S△PBD=
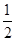 PB?BD=
PB?BD=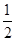 ×PB×4=4,
×PB×4=4,
∴BP=2,
∴P(2,6),
把P(2,6)分别代入y=kx+2和y=
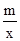 得:k=2,m=12,
得:k=2,m=12,∴一次函数的解析式是y=2x+2,反比例函数的解析式是y=
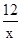 ,
,(3)由图形可知一次函数的值大于反比例函数值的x的取值范围是x>2.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目

 的解是______.
的解是______.
 、
、 分别表示父、子俩送票、取票过程中,离体育馆的路程
分别表示父、子俩送票、取票过程中,离体育馆的路程 (米)与所用时间
(米)与所用时间 (分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
(分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
 的坐标和
的坐标和 与
与 在同一坐标系中的图象大致是 ( )
在同一坐标系中的图象大致是 ( )
 和直线
和直线 的交点在第三象限,则m的取值范围是________.
的交点在第三象限,则m的取值范围是________.