题目内容
方程（3-x）（x+7）=12的根的情况是
- A.有两个不相等的实数根
- B.有两个相等的实数根
- C.没有实数根
- D.根的情况无法确定
A
分析：首先化成方程的一般形式得出x2+4x-9=0，求出b2-4ac的值即可．
解答：（3-x）（x+7）=12，
x2+4x-9=0，
b2-4ac=42-4×1×（-9）=52＞0，
∴方程有两个不相等的实数根．
故选A．
点评：本题主要考查对解一元二次方程，根的判别式等知识点的理解和掌握，能熟练地根据根的判别式进行判断是解此题的关键．
分析：首先化成方程的一般形式得出x2+4x-9=0，求出b2-4ac的值即可．
解答：（3-x）（x+7）=12，
x2+4x-9=0，
b2-4ac=42-4×1×（-9）=52＞0，
∴方程有两个不相等的实数根．
故选A．
点评：本题主要考查对解一元二次方程，根的判别式等知识点的理解和掌握，能熟练地根据根的判别式进行判断是解此题的关键．
练习册系列答案
同步练习强化拓展系列答案
相关题目
下列方程中，以x表示y的是（ ）
| A、x+y=8 | ||
B、x=
| ||
| C、2y=5x+7 | ||
| D、y=2x-1 |
关于x的分式方程
=
无解，则m的值为（ ）
| 2x |
| x+1 |
| m |
| x+1 |
| A、-2 | B、-1 | C、0 | D、2 |
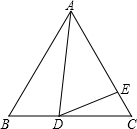已知：等边△ABC中，AB、cosB是关于x的方程x2-4mx-