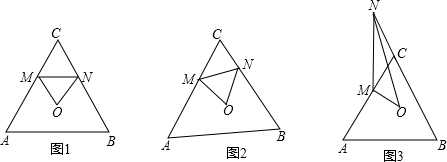
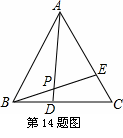
题目内容
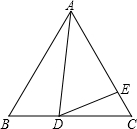 已知:等边△ABC中,AB、cosB是关于x的方程x2-4mx-
已知:等边△ABC中,AB、cosB是关于x的方程x2-4mx-| 1 | 2 |
分析:本题可先根据cosB的值求出AB的长,然后通过证△ABD和△DCE相似,得出关于AB,CD,BD,CE的比例关系式,即可得出关于y,x的函数关系式,然后根据函数的性质即可求出y的最小值.
解答:解:∵△ABC是等边三角形,
∴cosB=cos60°=
,
∴
,
解得:m1=0,m2=2,
∵
AB=m2≠0,
∵m=0不合题意,舍去;
∴m=2即AB=8,
∵∠ADE=60°,
∴∠ADB+∠CDE=120°,
又∠ADB+∠BAD=180°-∠B=120°,
∴∠BAD=∠CDE,
又∵∠B=∠C=60°,
∴△ABD∽△DCE,
∴
=
,
设BD=x,EA=y则DC=8-x,CE=8-y,
∴
=
,
∴y=
x2-x+8=
(x-4)2+6.
∴当BD=4,即D为BC的中点时,EA有最小值6.
∴cosB=cos60°=
| 1 |
| 2 |
∴
|
解得:m1=0,m2=2,
∵
| 1 |
| 2 |
∵m=0不合题意,舍去;
∴m=2即AB=8,
∵∠ADE=60°,
∴∠ADB+∠CDE=120°,
又∠ADB+∠BAD=180°-∠B=120°,
∴∠BAD=∠CDE,
又∵∠B=∠C=60°,
∴△ABD∽△DCE,
∴
| AB |
| DC |
| BD |
| CE |
设BD=x,EA=y则DC=8-x,CE=8-y,
∴
| 8 |
| 8-x |
| x |
| 8-y |
∴y=
| 1 |
| 8 |
| 1 |
| 8 |
∴当BD=4,即D为BC的中点时,EA有最小值6.
点评:本题考查了韦达定理,相似三角形的判定和性质,等边三角形的性质及二次函数的综合应用等知识点.
通过相似三角形得出与所求线段相关的比例关系式是解题的关键.
通过相似三角形得出与所求线段相关的比例关系式是解题的关键.

练习册系列答案
相关题目
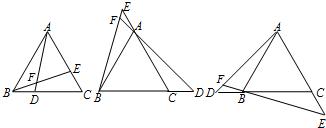
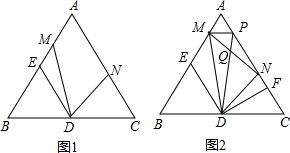 连DM,作DN平分∠MDC交AC于N.
连DM,作DN平分∠MDC交AC于N.