题目内容
【题目】如图,点P关于OA、OB的对称点分别为H、G,直线HG交OA、OB于点C、D,若∠HOG=80°,则∠CPD=___________.

【答案】100°
【解析】
要求∠CPD的度数,要在△CPD中进行,根据轴对称的性质和等腰三角形的性质找出与∠CPD的关系,利用已知可得∠AOB=40°可求出∠CPD.
解:连接OP
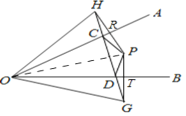
∵P关于OA、OB的对称点是H、G,
∴OA垂直平分PH于R,OB垂直平分PG于T,
∴CP=CH,DG=DP,
∴∠PCD=2∠CHP,∠PDC=2∠DGP,
∵∠PRC=∠PTD=90°,
∴在四边形OTPR中,
∴∠RPT+∠AOB=180°,
∵∠POC=∠COH,∠POD=∠DOG,∠HOG=80°,
∴∠AOB=40°
∴∠RPT=180°-40°=140°
∴∠CHP+∠PGD=40°,
∴∠PCD+∠PDC=80°
∴∠CPD=180°-80°=100°.
故答案为100°.

练习册系列答案
相关题目
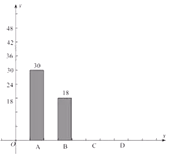
【题目】深圳市某学校抽样调查,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.
类型 | 频数 | 频率 |
A | 30 |
|
B | 18 | 0.15 |
C |
| 0.40 |
D |
|
|
(1)学生共________人, ![]() ________,
________, ![]() ________;
________;
(2)补全条形统计图;
(3)若该校共有2000人,骑共享单车的有________人.