题目内容
【题目】已知:如图,AB是⊙O的直径,AB=6,延长AB到点C,使BC=AB,D是⊙O上一点,DC= ![]() .求证:
.求证: 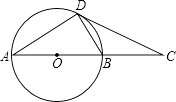
(1)△CDB∽△CAD;
(2)CD是⊙O的切线.
【答案】
(1)证明:∵AB=6,BC=AB,DC= ![]() ,
,
∴AC=12,BC=6.
∴ ![]() .
.
∵∠C=∠C,
∴△CDB∽△CAD
(2)证明:(证法一):连接OD,则有OD=3,
∵OC=9,DC= ![]() ,
,
∵DC2+OD2=(6 ![]() )2+32=81=92
)2+32=81=92
∴DC2+OD2=OC2
∴∠ODC=90°,
∴CD⊥OD.
又∵OD是半径,
∴CD是⊙O的切线.
(证法二):连接OD,则有OD=OA,
∴∠A=∠ADO.
∵△CDB∽△CAD,
∴∠CDB=∠A.
∴∠CDB=∠ADO.
∵AB是⊙O的直径,
∴∠ADB=90°.
即∠ADO+∠ODB=90°.
∴∠CDB+∠ODB=90°.
即∠ODC=90°.
∴CD⊥OD.
∵OD是半径,
∴CD是⊙O的切线.
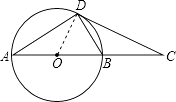
【解析】(1)根据已知及相似三角形的判定方法进行分析即可;(2)连接OD,求出OD2+CD2=OC2 , 根据勾股定理的逆定理得出∠ODC=90°,得出结论.
【考点精析】本题主要考查了切线的判定定理和相似三角形的判定的相关知识点,需要掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS)才能正确解答此题.

练习册系列答案
相关题目