��Ŀ����
����Ŀ���Ķ�������ϣ�
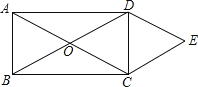
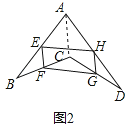
����ѧ���ϣ���ʦ��ͬѧ˼���������⣺��ͼ1�����ǰ�һ���ı���ABCD���ı��е�E��F��G��H�������������õ����ı���EFGH��ƽ���ı�����
С����˼�������ǣ�������˼·������AC��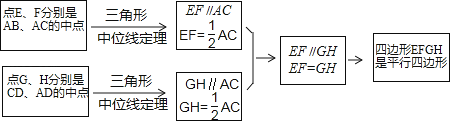
���С����˼·����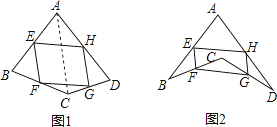
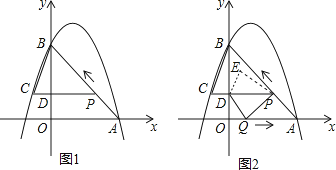
��1����ֻ�ı�ͼ1���ı���ABCD����״����ͼ2�������ı���EFGH����ƽ���ı�����˵�����ɣ��ο�С��˼�����ⷽ�����һ�����⣺
��2����ͼ2���ڣ�1���������£�������AC��BD��
�ٵ�AC��BD����ʲô����ʱ���ı���EFGH�����Σ�д�����۲�֤����
�ڵ�AC��BD����ʲô����ʱ���ı���EFGH�Ǿ��Σ�ֱ��д�����ۣ�
���𰸡�
��1��
�⣺��ƽ���ı��Σ�
֤������ͼ2������AC��
��E��AB���е㣬F��BC���е㣬
��EF��AC��EF= ![]() AC��
AC��
ͬ��HG��AC��HG= ![]() AC��
AC��
���Ͽɵã�EF��HG��EF=HG��
���ı���EFGH��ƽ���ı���
��2��
�⣺��AC=BD��
�������£�
�ɣ�1��֪���ı���EFGH��ƽ���ı��Σ���FG= ![]() BD��HG=
BD��HG= ![]() AC��
AC��
�൱AC=BDʱ��FG=HG��
��ƽ���ı���EFGH������
�ڵ�AC��BDʱ���ı���EFGHΪ���Σ�
�������£�
ͬ��2���ã��ı���EFGH��ƽ���ı��Σ�
��AC��BD��GH��AC��
��GH��BD��
��GF��BD��
��GH��GF��
���HGF=90�㣬
���ı���EFGHΪ���Σ�
����������1����ͼ2������AC��������������λ�ߵ����ʵõ�EF��AC��EF= ![]() AC��Ȼ�����ƽ���ı����ж��������ɵõ����ۣ���2���ɣ�1��֪���ı���EFGH��ƽ���ı��Σ���FG=
AC��Ȼ�����ƽ���ı����ж��������ɵõ����ۣ���2���ɣ�1��֪���ı���EFGH��ƽ���ı��Σ���FG= ![]() BD��HG=
BD��HG= ![]() AC�����ǵõ���AC=BDʱ��FG=HG�����ɵõ����ۣ���3������ƽ���ߵ����ʵõ�GH��BD��GH��GF�����ǵõ���HGF=90�㣬���ݾ��ε��ж��������ɵõ����ۣ�������Ҫ�������е��ı��Σ��ؼ���������������λ�߶����������ε���λ��ƽ���ڵ������ҵ��ڵ����ߵ�һ�룮
AC�����ǵõ���AC=BDʱ��FG=HG�����ɵõ����ۣ���3������ƽ���ߵ����ʵõ�GH��BD��GH��GF�����ǵõ���HGF=90�㣬���ݾ��ε��ж��������ɵõ����ۣ�������Ҫ�������е��ı��Σ��ؼ���������������λ�߶����������ε���λ��ƽ���ڵ������ҵ��ڵ����ߵ�һ�룮

 Сѧ���AB��ϵ�д�
Сѧ���AB��ϵ�д�����Ŀ���ڶ����»�У�ijУ����ȫ��ʦ���������飬Ϊ�˽������鼮�����࣬ͼ�����Ա�Բ����鼮�����˳������飬���ݵ������ݻ��������²�������ͳ��ͼ�����������ͳ��ͼ�����ṩ����Ϣ�ش��������⣺
ijУʦ�������������ͳ�Ʊ�
���� | Ƶ�� | �ٷֱ� |
A�������� | 12 | n |
B����ѧ�� | 14 | 35% |
C�������� | m | 20% |
D�������� | 6 | 15% |
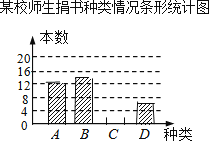
��1��ͳ�Ʊ��е�m= �� n=��
��2����ȫ����ͳ��ͼ��
��3�����λʦ��������2000����������ж��ٱ�������ͼ�飿