��Ŀ����
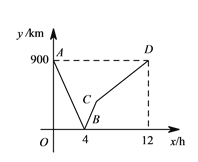
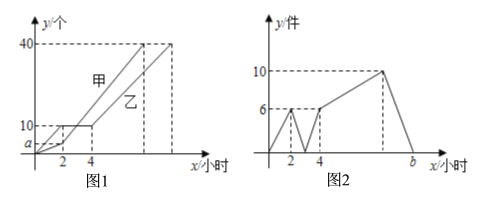
����Ŀ���ס������˷ֱ�װͬһ�����40�����������ڰ�װ��Сʱ����Ϣ��2Сʱ���������ԭ�����ȹ���������ÿ�˰�װ���������y�������밲װʱ��x��Сʱ���ĺ�����ϵ��ͼ1��ʾ�����˰�װ�������֮��z��������ʱ��x��Сʱ���ĺ�����ϵ��ͼ2��ʾ��
��1��a���� ����b���� ����
��2���������2Сʱ��İ�װ�������y��ʱ��x�ĺ�����ϵ��
��3���ס���������ʲôʱ������������������8����
���𰸡���1��4�� 10����2��y��6x��8��2��x��8������3��6Сʱ��8.4Сʱ.
��������
��1������ͼ����a��ֵ��ͼ1��֪4Сʱ��һֱ�������ȣ���������ɣ�����ֻ�е���Ҳ�������ʱ�����˰�װ�������֮��Ż�Ϊ0�������ҵĹ���Ч�ʼ������b��ֵ��
��2������ͼ���������2Сʱ���ͼ����![]() �͵�
�͵�![]() ���ô���ϵ�������ɵã�
���ô���ϵ�������ɵã�
��3������ͼ��������4Сʱ������������������Ŵﵽ8�����ٸ��ݼס��ҵĹ���Ч�ʣ�����ڼ��������֮ǰ�ͼ��������֮����������������г���ʽ��⼴��.
��1����ͼ�ɵã�![]() ��
��
ͼ1��֪4Сʱ��һֱ�������ȣ���������ɣ�����ֻ�е���Ҳ�������ʱ�����˰�װ�������֮��Ż�Ϊ0���ҵĹ���Ч��Ϊ![]() ��/Сʱ��
��/Сʱ��
��![]() ��
��
��2������4Сʱ���˰�װ�������֮��ɵã�4Сʱ�װ�װ���������Ϊ![]() ����
����
�����2Сʱ��İ�װ�������y��ʱ��x�ĺ�����ϵ��![]() ��
��
����2Сʱ��İ�װ�������y��ʱ��x�ĺ���ͼ�����![]() �͵�
�͵�![]() ��
��
�����![]() �����
�����![]() ��
��
![]()
��![]() ��
��![]() �����
�����![]() ��
��
�ʼ���2Сʱ��İ�װ�������y��ʱ��x�ĺ�����ϵ��![]() ��
��
��3����tСʱ�ס�����������������������8����
��ͼ2��![]() ��
��
2Сʱ��Ĺ���Ч��Ϊ��![]() ��/Сʱ��
��/Сʱ��
���ڼ����֮ǰ����![]() ʱ��
ʱ��![]()
���![]() ��
��
���ڼ����֮��![]() ʱ��
ʱ��![]() ��
��
���![]()
�𣺼ס���������6Сʱ��8.4Сʱʱ����������������8��.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��Ϊ����ѧ�������Ķ���ϰ�ߣ���ѧУ�ձ鿪չ�ˡ��ҵ���.�й��Ρ������Ķ����ijУΪ�˽����꼶1200��ѧ���������Ķ�����ʱ������������������˲���ͬѧ�����������ͳ�ƣ����������Ƴ����²�������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ�������ͼ����Ϣ����������⣺
��1������ a= ��b= ��
��2���벹ȫƵ���ֲ�ֱ��ͼ�п�ȱ�IJ��֣�
��3�������У�ѧ�����Ķ�����ʱ�����λ�����ڵ� �飻
��4������Ƹ�У���꼶ѧ�����Ķ������� 1 Сʱ��������
��� | ʱ��Σ�Сʱ�� | Ƶ�� | Ƶ�� |
1 | 0��x��0.5 | 10 | 0.05 |
2 | 0.5��x��1.0 | 20 | 0.10 |
3 | 1.0��x��1.5 | 80 | b |
4 | 1.5��x��2.0 | a | 0.35 |
5 | 2.0��x��2.5 | 12 | 0.06 |
6 | 2.5��x��3.0 | 8 | 0.04 |