题目内容
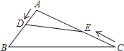
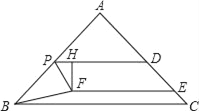
【题目】如图,在△ABC中,AB=AC=5,BC=6,动点P从点A出发沿AB向点B移动,(点P与点A、B不重合),作PD∥BC交AC于点D,在DC上取点E,以DE、DP为邻边作平行四边形PFED,使点F到PD的距离![]() ,连接BF,设AP=x.
,连接BF,设AP=x.
(1)△ABC的面积等于 ;
(2)设△PBF的面积为y,求y与x的函数关系,并求y的最大值.
(3)当BP=BF时,求x的值.
【答案】(1)12;(2)当x=![]() 时,y取得最大值,最大值为
时,y取得最大值,最大值为![]() ;(3)x=
;(3)x=![]()
【解析】
(1)根据题意,易得△ABC的高,再由三角形面积公式可得答案;
(2)根据平行线的性质,可得PD、PM的值,进而可得AN的值,再由图示可得:y=S梯形PBCD-SPFED-S梯形PFCE;代入数据可得答案.
(3)过B作BT⊥AC于T交PF于K,由(2)得出的关系可知△AND∽△AGE,利用三角形面积,得到BT的值,继而得到cos∠A的值,最后得到x的值.
(1)根据题意,作AQ⊥BC,交BC于点Q,
易得:BQ=3,由勾股定理,易得AQ=4;
则![]()
(2)设AQ与PD交于点M,与EF交于点N;
PD∥BC,
∴△APD∽△ABC,
∴![]()
且AP=x,AB=5,BC=6,
可得: ![]()
易得![]() ,则AN=AM+MN=AM+HF=x,
,则AN=AM+MN=AM+HF=x,
∴y=S梯形PBCD﹣SPFED﹣S梯形BFEC
![]()
故当x=![]() 时,y取得最大值,最大值为
时,y取得最大值,最大值为![]() .
.
(3)过B作BT⊥AC于T交PF于K,
∵PF∥AC,则BK⊥PF于K,由(2)知道
![]()
∴△AND∽△AGE,
∴![]()
∴![]()
∴![]()
在△ABC中,![]() ∴
∴![]()
在Rt△ABT中,由勾股定理得![]() ,∴cos∠A
,∴cos∠A![]()
若BP=BF,则三线合一,![]()
在Rt△BPK中cos∠BPK![]() ,
,
∴![]()
解得![]()

练习册系列答案
相关题目