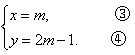题目内容
阅读材料:当抛物线的解析式中含有字母系数时,随着系数中的字母取值的不同,抛物线的顶点坐标也将发生变化.例如:由抛物线y=x2-2mx+m2+2m-1,配方得y=(x-m)2+2m-1,∴抛物线顶点坐标为(m,2m-1).即
,当m的值变化时,x,y的值也随之变化,因而y的值也随x值的变化而变化.将(1)代(2),得y=2x-1.可见,不论m取任何实数,抛物线顶点的纵坐标y和横坐标x都满足关系式:y=2x-1;根据阅读材料提供的方法,确定抛物线y=x2-2mx+2m2-3m+1顶点的纵坐标y与横坐标x之间的关系式.
|
分析:把抛物线解析式配方成顶点式解析式,再写出顶点坐标,然后消掉m整理即可得解.
解答:解:由y=x2-2mx+2m2-3m+1,
配方得y=(x-m)2+m2-3m+1,
∴抛物线顶点坐标为(m,m2-3m+1),
即
,
当m的值变化时,x,y的值也随之变化,因而y的值也随x值的变化而变化.
将①代入②,得y=x2-3x+1,
因此,抛物线y=x2-2mx+2m2-3m+1顶点的纵坐标y与横坐标x之间的关系式为:y=x2-3x+1.
配方得y=(x-m)2+m2-3m+1,
∴抛物线顶点坐标为(m,m2-3m+1),
即
|
当m的值变化时,x,y的值也随之变化,因而y的值也随x值的变化而变化.
将①代入②,得y=x2-3x+1,
因此,抛物线y=x2-2mx+2m2-3m+1顶点的纵坐标y与横坐标x之间的关系式为:y=x2-3x+1.
点评:本题考查了二次函数的性质,配方法的应用,读懂题目信息,理解顶点所在直线的求解方法是解题的关键.

练习册系列答案
相关题目
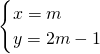 ,当m的值变化时,x,y的值也随之变化,因而y的值也随x值的变化而变化.将(1)代(2),得y=2x-1.可见,不论m取任何实数,抛物线顶点的纵坐标y和横坐标x都满足关系式:y=2x-1;根据阅读材料提供的方法,确定抛物线y=x2-2mx+2m2-3m+1顶点的纵坐标y与横坐标x之间的关系式.
,当m的值变化时,x,y的值也随之变化,因而y的值也随x值的变化而变化.将(1)代(2),得y=2x-1.可见,不论m取任何实数,抛物线顶点的纵坐标y和横坐标x都满足关系式:y=2x-1;根据阅读材料提供的方法,确定抛物线y=x2-2mx+2m2-3m+1顶点的纵坐标y与横坐标x之间的关系式.