题目内容
【题目】已知,![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() .
.
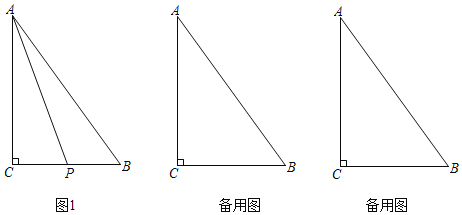
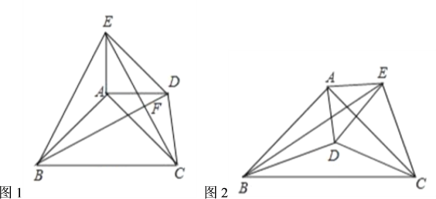
(1)如图1,点![]() 、
、![]() 都在
都在![]() 外部,连接
外部,连接![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 与
与![]() 相交于
相交于![]() 点,判断
点,判断![]() 与
与![]() 的关系,说明理由,若
的关系,说明理由,若![]() ,求四边形
,求四边形![]() 的面积;
的面积;
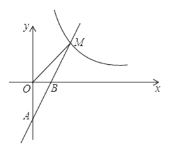
(2)如图2,点![]() 在
在![]() 内部,点
内部,点![]() 在
在![]() 的外部,连接
的外部,连接![]() 、
、![]() 、
、![]() 、
、![]() ,当
,当![]() ,
,![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)BD=CE,BD⊥CE;50;(2)10
【解析】
(1)证明△ABD≌△ACE,可得BD=CE,∠ABD=∠ACE,证出BD⊥CE,根据S四边形BCDE=S△BCE+S△DCE可求出答案;
(2)延长BD交AC于点O,交CE于点F,同(1)可得△ABD≌△ACE,可证出BD⊥CE,得出BE2+CD2=BC2+DE2,即可求解.
解:(1)BD=CE,BD⊥CE,理由如下:
∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,
∵∠BAD=∠BAC+∠DAC,∠CAE=∠DAE+∠DAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠ABD=∠ACE,
∵∠ABD+∠DBC=90°,
∴∠DBC+∠ACE=90°,
∴∠BFC=90°,即BD⊥CE;
∴S四边形BCDE=S△BCE+S△DCE=![]() ×CE×BF+
×CE×BF+![]() ×CE×DF=
×CE×DF=![]() ×CE×BD=
×CE×BD=![]() ×10×10=50;
×10×10=50;
(2)延长BD交AC于点O,交CE于点F,
同(1)△ABD≌△ACE,
∴∠ABD=∠ACE,
∵∠AOB=∠COF,
∴∠BAC=∠BFC=90°,
∴BD⊥CE,
∴BE2=BF2+EF2,CD2=CF2+DF2,
∴BE2+CD2=BF2+EF2+CF2+DF2,
∵BF2+CF2=BC2,DF2+EF2=DE2,
∴BE2+CD2=BC2+DE2,
∵AE=1,AC=2,
∴DE=![]() AE=
AE=![]() ,BC=
,BC=![]() AC=2
AC=2![]() ,
,
∴BE2+CD2=(2![]() )2+(
)2+(![]() )2=8+2=10.
)2=8+2=10.


【题目】某宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如下表:
x(元) | 180 | 260 | 280 | 300 |
y(间) | 100 | 60 | 50 | 40 |
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每间空置的客房,宾馆每日需支出各种费用60元.当房价为多少元时,宾馆当日利润最大?求出最大利润.(宾馆当日利润=当日房费收入-当日支出)