题目内容
下列说法:①
 是二次根式,但不是整式;
是二次根式,但不是整式;②方程
 是一元二次方程;
是一元二次方程;③若ac<0,则方程ax2+bx+c=0必有两个不相等的实数根;
④数学课本第40页观察与猜想讨论了一元二次方程根与系数的关系,根据这一关系得方程x2-3x+5=0的两根和是3,两根积是5.
其中错误的有( )
A.3个
B.2个
C.1个
D.0个
【答案】分析:首先根据二次根式与整式的定义,即可判定①错误;由一元二次方程的定义(只含有一个未知数,并且未知数的最高次数是2的整式方程叫一元二次方程)即可判定②错误;由判别式△=b2-4ac>0,即可判定方程ax2+bx+c=0必有两个不相等的实数根,即可得③正确;由根与系数的关系是在方程有跟的情况下分析的,可得④错误;继而求得答案.
解答:解:①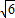 是二次根式,而且是常数,所以是整式;故①错误;
是二次根式,而且是常数,所以是整式;故①错误;
②∵方程3x2-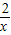 =0不是整式方程,∴不是一元二次方程;故②错误;
=0不是整式方程,∴不是一元二次方程;故②错误;
③∵b2≥0,ac<0,
∴△=b2-4ac>0,
∴方程ax2+bx+c=0必有两个不相等的实数根;
故③正确;
④∵△=b2-4ac=(-3)2-4×1×5=9-20=-11<0,
∴方程x2-3x+5=0无解,
而根与系数的关系是在方程有解的情况下分析的,
故④错误.
∴错误的有3个.
故选A.
点评:此题考查了一元二次方程的定义、根的判别式的知识、根与系数的关系以及二次根式、整式的概念等知识.此题综合性较强,难度适中,解题的关键是准确理解各定义的含义.
解答:解:①
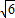 是二次根式,而且是常数,所以是整式;故①错误;
是二次根式,而且是常数,所以是整式;故①错误;②∵方程3x2-
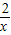 =0不是整式方程,∴不是一元二次方程;故②错误;
=0不是整式方程,∴不是一元二次方程;故②错误;③∵b2≥0,ac<0,
∴△=b2-4ac>0,
∴方程ax2+bx+c=0必有两个不相等的实数根;
故③正确;
④∵△=b2-4ac=(-3)2-4×1×5=9-20=-11<0,
∴方程x2-3x+5=0无解,
而根与系数的关系是在方程有解的情况下分析的,
故④错误.
∴错误的有3个.
故选A.
点评:此题考查了一元二次方程的定义、根的判别式的知识、根与系数的关系以及二次根式、整式的概念等知识.此题综合性较强,难度适中,解题的关键是准确理解各定义的含义.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目