题目内容
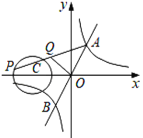
【题目】如图,一次函数y=3x与反比例函数y=![]() 的图象交于点A,B,点P在以C(﹣4,0)为圆心,1为半径的⊙C上,Q是AP的中点,若OQ长的最大值为
的图象交于点A,B,点P在以C(﹣4,0)为圆心,1为半径的⊙C上,Q是AP的中点,若OQ长的最大值为![]() ,则k的值为_____.
,则k的值为_____.
【答案】![]()
【解析】
作辅助线,先确定OQ长的最大时,点P的位置,当BP过圆心C时,BP最长,设B(t,3t),则CD=t(4)=t+4,BD=3t,根据勾股定理计算t的值,可得k的值.
解:如图,连接BP,
由对称性得:OA=OB,
∵Q是AP的中点,
∴OQ=![]() BP,
BP,
∵OQ长的最大值为![]()
∴BP长的最大值为2×![]() =5,
=5,
如图,当BP过圆心C时,BP最长,过B作BD⊥x轴于D,
∵CP=1,
∴BC=BP-1=4,
∵B在直线y=3x上,
设B(t,3t),则CD=t(4)=t+4,BD=3t,
在Rt△BCD中,由勾股定理得:BC2=CD2+BD2,
∴42=(t+4)2+(3t)2,
解得t=0(舍)或![]() ,
,
∴B(![]() ,
,![]() ),
),
∵点B在反比例函数y=![]() (k>0)的图象上,
(k>0)的图象上,
∴k=(![]() )×(
)×(![]() )=
)=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目