题目内容
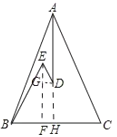
【题目】如图,在△ABC中,AB=AC,D,E是△ABC内的两点,AD平分∠BAC,∠EBC=∠E=60°.若BE=9cm,DE=3cm,则BC的长为 ( )

A.12cmB.11cmC.9cmD.6cm
【答案】A
【解析】
过点E作EF⊥BC,垂足为F,延长AD到H,交BC于点H,过点D作DG⊥EF,垂足为G,由直角三角形中30°所对的直角边是斜边的一半可知BF=4.5,DG=1.5,然后由等腰三角形三线合一可知AH⊥BC,BH=CH,然后再证明四边形DGFH是矩形,从而得到FH=GD=1.5,最后根据BC=2BH计算即可.
过点E作EF⊥BC,垂足为F,延长AD到H,交BC于点H,过点D作DG⊥EF,垂足为G.
∵EF⊥BC,∠EBF=60°,
∴∠BEF=30°,
∴BF=![]() BE=
BE=![]() ×9=4.5,
×9=4.5,
∵∠BED=60°,∠BEF=30°,
∴∠DEG=30°.
又∵DG⊥EF,
∴GD=![]() ED=
ED=![]() ×3=1.5,
×3=1.5,
∵AB=AC,AD平分∠BAC,
∴AH⊥BC,且BH=CH.
∵AH⊥BC,EF⊥BC,DG⊥EF,
∴四边形DGFH是矩形.
∴FH=GD=1.5.
∴BC=2BH=2×(4.5+1.5)=12.
故选:A.

练习册系列答案
相关题目







