题目内容
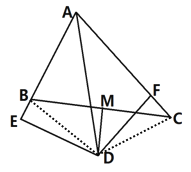
【题目】如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于D,DE⊥AB交AB的延长线于E,DF⊥AC,现有下列结论:①DE=DF; ②DE+DF=AD; ③DM平分∠ADF; ④AB+AC=2AE,其中正确的个数有( )

A.1个B.2个C.3个D.4个
【答案】C
【解析】
①由角平分线的性质可知①正确;②由题意可知∠EAD=∠FAD=30°,故可得ED=![]() AD,DF=
AD,DF=![]() AD,从而可证明②正确;③若DM平分∠ADF,则∠EDM=90°,从而得到∠ABC为直角三角形,条件不足,不能确定,故③错误;④证明△EBD≌△DFC和Rt△AED≌Rt△AFD,从而得到BE=FC,AE=AF,进而可证明④正确.
AD,从而可证明②正确;③若DM平分∠ADF,则∠EDM=90°,从而得到∠ABC为直角三角形,条件不足,不能确定,故③错误;④证明△EBD≌△DFC和Rt△AED≌Rt△AFD,从而得到BE=FC,AE=AF,进而可证明④正确.
解:如图所示:连接BD、DC.
①∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
∴①正确;
②∵∠EAC=60°,AD平分∠BAC,
∴∠EAD=∠FAD=30°,
∵DE⊥AB,
∴∠AED=90°,
∴ED=![]() AD,
AD,
同理:DF=![]() AD,
AD,
∴DE+DF=AD,
∴②正确;
③由题意可知:∠EDA=∠ADF=60°,
假设DM平分∠ADF,则∠ADM=30°,则∠EDM=90°,
又∵∠E=∠BMD=90°,
∴∠EBM=90°,
∴∠ABC=90°,
∵不知道∠ABC是否等于90°,
∴不能判定DM平分∠ADF,
∴③错误;
④∵DM是BC的垂直平分线,
∴DB=DC,
在Rt△BED和Rt△CFD中,![]() ,
,
∴Rt△BED≌Rt△CFD(HL),
∴BE=FC,
同理可证,Rt△AED≌Rt△AFD,
∴AE=AF,
∴AB+AC=AEBE+AF+FC=2AE,
∴④正确,
故选:C.

练习册系列答案
相关题目







