题目内容
 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°.点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA.则下列结论:①若∠MFC=130°,则∠MAB=40°;②∠MPB=90°-
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°.点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA.则下列结论:①若∠MFC=130°,则∠MAB=40°;②∠MPB=90°- ∠FCM;③△ABM∽△CEF;④S四边形AMED-S△EFC;=2S△MFC′.正确的是
∠FCM;③△ABM∽△CEF;④S四边形AMED-S△EFC;=2S△MFC′.正确的是
- A.①②④
- B.①③④
- C.②③
- D.①②③④
D
分析:连接DF,根据线段的垂直平分线的性质,以及CF=AD,MF=MA,即可证明△AMD≌△FMD≌△FMC,根据相似三角形的性质即可判断.
解答: 解:连接DF.
解:连接DF.
(1)∵ME⊥CD,E为CD中点
∴ME垂直平分CD
∴MC=MD
又∵CF=DA,MF=MA
∴△CMF≌△DMA
∴∠MAD=∠MFC=130°
又∵∠BAD=90°
∴∠MAB=40°
故①正确;
∴AM=2MB
(2)∵△CMF≌△DMA
∴∠FCM=∠ADM
又∵AD‖BC
∴∠CMD=∠ADM=∠FCM
∵MC=MD,ME为CD边中垂线
∴ME为∠DMC的角平分线
∴∠BMP= ∠CMD=
∠CMD= ∠FCM
∠FCM
又∵AB⊥BC
∴∠MPB+∠BMP=90°
∴∠MPB=90°- ∠FCM
∠FCM
故②正确;
连接DF,则△AMD≌△FMD≌△FMC,
∴S△AMD=S△FMD=S△FMC
∴S四边形AMED-S△AMD-S△FMD=S△DEF
又∵S△DEF=S△EFC
∴S四边形AMED-S△EFC;=2S△MFC
故④正确;
∵∠AMD=∠DMP=∠EMC,∠EFC=∠FMC+∠FCM
∴∠AMB=∠EFC
∵∠ABM=∠MEC
∴△ABM∽△CEF
故③正确.
故正确的是①②③④.
故选D.
点评:本题主要考查了线段的垂直平分线的性质以及三角形全等的判定和性质,注意到△AMD≌△FMD≌△FMC是解决本题的关键.
分析:连接DF,根据线段的垂直平分线的性质,以及CF=AD,MF=MA,即可证明△AMD≌△FMD≌△FMC,根据相似三角形的性质即可判断.
解答:
 解:连接DF.
解:连接DF.(1)∵ME⊥CD,E为CD中点
∴ME垂直平分CD
∴MC=MD
又∵CF=DA,MF=MA
∴△CMF≌△DMA
∴∠MAD=∠MFC=130°
又∵∠BAD=90°
∴∠MAB=40°
故①正确;
∴AM=2MB
(2)∵△CMF≌△DMA
∴∠FCM=∠ADM
又∵AD‖BC
∴∠CMD=∠ADM=∠FCM
∵MC=MD,ME为CD边中垂线
∴ME为∠DMC的角平分线
∴∠BMP=
 ∠CMD=
∠CMD= ∠FCM
∠FCM 又∵AB⊥BC
∴∠MPB+∠BMP=90°
∴∠MPB=90°-
 ∠FCM
∠FCM故②正确;
连接DF,则△AMD≌△FMD≌△FMC,
∴S△AMD=S△FMD=S△FMC
∴S四边形AMED-S△AMD-S△FMD=S△DEF
又∵S△DEF=S△EFC
∴S四边形AMED-S△EFC;=2S△MFC
故④正确;
∵∠AMD=∠DMP=∠EMC,∠EFC=∠FMC+∠FCM
∴∠AMB=∠EFC
∵∠ABM=∠MEC
∴△ABM∽△CEF
故③正确.
故正确的是①②③④.
故选D.
点评:本题主要考查了线段的垂直平分线的性质以及三角形全等的判定和性质,注意到△AMD≌△FMD≌△FMC是解决本题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
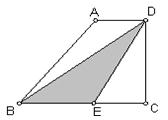 20、如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E为BC边上的点.将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合(如图中阴影所示).若∠A=130°,AB=4cm,则梯形ABCD的高CD≈
20、如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E为BC边上的点.将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合(如图中阴影所示).若∠A=130°,AB=4cm,则梯形ABCD的高CD≈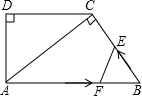 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).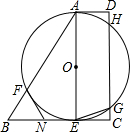 (1998•大连)如图,在直角梯形ABCD中.AD∥BC,DC⊥BC,且BC=3AD.以梯形的高AE为直径的⊙O交AB于点F,交CD于点G、H.过点F引⊙O的切线交BC于点N.
(1998•大连)如图,在直角梯形ABCD中.AD∥BC,DC⊥BC,且BC=3AD.以梯形的高AE为直径的⊙O交AB于点F,交CD于点G、H.过点F引⊙O的切线交BC于点N. BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.
BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.