题目内容
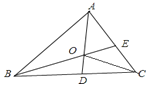
【题目】如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M.

(1)求证:∠FMC=∠FCM;
(2)AD与MC垂直吗?并说明理由.
【答案】(1)证明见解析(2)垂直,理由见解析
【解析】
试题分析:(1)根据等腰直角三角形的性质得出DF⊥AE,DF=AF=EF,进而利用全等三角形的判定得出△DFC≌△AFM(AAS),即可得出答案;
(2)由(1)知,∠MFC=90°,FD=EF,FM=FC,即可得出∠FDE=∠FMC=45°,即可理由平行线的判定得出答案.
(1)证明:∵△ADE是等腰直角三角形,F是AE中点,
∴DF⊥AE,DF=AF=EF,
又∵∠ABC=90°,
∠DCF,∠AMF都与∠MAC互余,
∴∠DCF=∠AMF,
在△DFC和△AFM中,
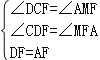 ,
,
∴△DFC≌△AFM(AAS),
∴CF=MF,
∴∠FMC=∠FCM;
(2)AD⊥MC,
理由:由(1)知,∠MFC=90°,FD=FA=FE,FM=FC,
∴∠FDE=∠FMC=45°,
∴DE∥CM,
∴AD⊥MC.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某企业车间有50名工人,某一天他们生产的机器零件个数统计如表:
零件个数(个) | 6 | 7 | 8 |
人数(人) | 15 | 22 | 10 |
表中表示零件个数的数据中,众数、中位数分别是( )
A.7个、7个B.6个、7个C.5个、6个D.8个、6个