题目内容
【题目】如图,直线AB∥CD,点E、M分别为直线AB、CD上的点,点N为两平行线间的点,连接NE、NM,过点N作NG平分∠ENM,交直线CD于点G,过点N作NF⊥NG,交直线CD于点F,若∠BEN=160°,则∠NGD﹣∠MNF=__度.

【答案】110.
【解析】
过N点作NH∥AB,则AB∥NH∥CD,由平行线的性质得∠BEN+∠ENG+∠GNM+∠MNF+∠NFG=360![]() ,进而由NG平分∠ENM和∠BEN=160
,进而由NG平分∠ENM和∠BEN=160![]() 得∠GNM+∠GNM+∠MNF+∠NFG=200
得∠GNM+∠GNM+∠MNF+∠NFG=200![]() ,再由得∠GNM+∠NFG=110
,再由得∠GNM+∠NFG=110![]() ,进而由外角定理得结果.
,进而由外角定理得结果.
过N点作NH∥AB,则AB∥NH∥CD,
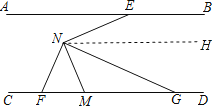
∴∠BEN+∠ENH=∠HNF+∠NFG=180![]() ,
,
∴∠BEN+∠ENH+∠HNF+∠NFG=360![]() ,
,
∴∠BEN+∠ENG+∠GNM+∠MNF+∠NFG=360![]() ,
,
∵∠BEN=160![]() ,
,
∴∠ENG+∠GNM+∠MNF+∠NFG=200![]() ,
,
∵NG平分∠ENM,
∴∠ENG=∠GNM,
∴∠GNM+∠GNM+∠MNF+∠NFG=200![]() ,
,
∵NF⊥NG,
∴∠GNM+∠MNF=∠GNF=90![]() ,
,
∴∠GNM+90°+∠NFG=200![]() ,
,
∴∠GNM+∠NFG=110![]() ,
,
∵∠NGD=∠GNM+∠MNF+∠NFG,
∴∠NGD﹣∠MNF=∠GNM+∠NFG=110![]() .
.
故答案为:110.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案【题目】问题:探究函数![]() 的图象与性质.
的图象与性质.
小明根据学习函数的经验,对函数![]() 的图象与性质进行了研究.
的图象与性质进行了研究.
下面是小明的研究过程,请补充完成.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
| … | -4 | -3 | -2 | -1 | 0 |
|
|
| 4 | … |
| … | 2 | 1 | 0 | n | 0 | 1 | m | 3 | 4 | … |
其中,m= n= ;
(2)在如图所示的平面直角坐标中,描出以上表中各对对应值为坐标的点,并根据描出的点,画出该函数的图象.
(3)观察图象,写出该函数的两条性质.