题目内容
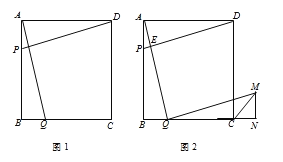
【题目】将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=![]() ,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )
,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )

A. ![]() B. 3 C. 2 D. 2
B. 3 C. 2 D. 2![]()
【答案】B
【解析】试题分析:由三角函数易得BE,AE长,根据翻折和对边平行可得△AEC1和△CEC1为等边三角形,那么就得到EC长,相加即可.
解:连接CC1.

在Rt△ABE中,∠BAE=30°,AB=![]() ,
,
∴BE=AB×tan30°=1,AE=2,∠AEB1=∠AEB=60°,
∵四边形ABCD是矩形
∴AD∥BC,
∴∠C1AE=∠AEB=60°,
∴△AEC1为等边三角形,
同理△CC1E也为等边三角形,
∴EC=EC1=AE=2,
∴BC=BE+EC=3,
故选B.

练习册系列答案
相关题目