题目内容
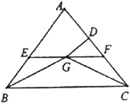
【题目】如图,在△ ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF ∥BC交AB于E,交AC于F,过点G作GD⊥ AC于D,下列四个结论:①EF = BE+CF;②∠BGC= 90 °+![]() ∠A;③点G到△ ABC各边的距离相等;④设GD =m,AE + AF =n,则S△AEF=
∠A;③点G到△ ABC各边的距离相等;④设GD =m,AE + AF =n,则S△AEF=![]() mn.其中正确的结论有( )
mn.其中正确的结论有( )
A.1 个B.2 个C.3 个D.4 个
【答案】D
【解析】
根据BG,CG分别是∠ABC和∠ACB的平分线,EF ∥BC,可得EB=EG,FG=FC,从而证得①正确;根据三角形内角和定理即可求出②正确;根据角平分线的性质可知点G是△ABC的内心,从而可得③正确;连接AG,结合点G是内心,即可表示出△AEG和△AFG的面积,从而可知④正确.
∵BG,CG分别是∠ABC和∠ACB的平分线,
∴∠EBG=∠GBC,∠FCG=∠GCB
∵EF ∥BC
∴∠EGB=∠GBC,∠FGC=∠GCB
∴∠EBG=∠EGB,∠FCG=∠FGC
∴EB=EG,FG=FC
∴EF = BE+CF
故①正确;
在△ABC中,∠A=180°-(∠ABC+∠ACB)
在△GBC中,![]() ,
,
即![]()
所以②正确;
∵点G是∠ABC和∠ACB的平分线的交点,
∴点G是△ABC的内心
∴点G到△ABC各边的距离相等
故③正确;

连接AG,
∵点G到△ABC各边的距离相等,GD=m,AE+AF=n,
∴![]()
故④正确;
综上答案选D.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目