题目内容
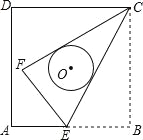
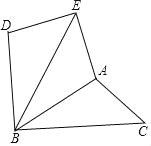
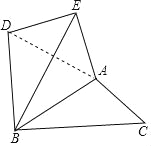
【题目】如图所示,∠DBC=90°,∠C=45°,AC=2,△ABC绕点B逆时针旋转60°得到△DBE,连接AE.
(1)求证:△ABC≌△ABE;
(2)连接AD,求AD的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)根据旋转的性质得到∠DBE=∠ABC,∠EBC=60°,BE=BC,根据全等三角形的判定定理即可得到结论;
(2)连接AD,根据旋转的性质得到DE=AC,∠BED=∠C,DE=AC=2,根据全等三角形的性质得到∠BEA=∠C,AE=AC=2,根据等腰三角形的性质即可得到结论.
(1)证明:∵△ABC绕点B逆时针旋转60°得到△DBE,
∴∠DBE=∠ABC,∠EBC=60°,BE=BC,
∵∠DBC=90°,
∴∠DBE=∠ABC=30°,
∴∠ABE=30°,
在△ABC与△ABE中,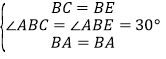 ,
,
∴△ABC≌△ABE(SAS);
(2)解:连接AD,
∵△ABC绕点B逆时针旋转60°得到△DBE,
∴DE=AC,∠BED=∠C,DE=AC=2,
∵△ABC≌△ABE,
∴∠BEA=∠C,AE=AC=2,
∵∠C=45°,
∴∠BED=∠BEA=∠C=45°,
∴∠AED=90°,DE=AE,
∴AD=![]() AE=2
AE=2![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目