题目内容
用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形.设格点多边形的面积为S,它各边上格点的个数和为x.
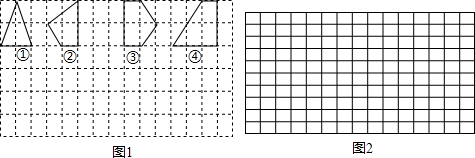
(1)上图中的格点多边形.其内部都只有1个格点,它们的面积与各边上格点的个数和的对应关系如下表,请写出S与x之间的关系式.
答:S=
x
x.
(2)请你再画出一些格点多边形,使这些多边形内部都有而且只有2个格点.此时所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式是:S=
x+1
x+1.
(3)请你继续探索,当格点多边形内部有且只有N个格点时,猜想S与x有怎样的关系.答:S=
x+(N-1)
x+(N-1).

(1)上图中的格点多边形.其内部都只有1个格点,它们的面积与各边上格点的个数和的对应关系如下表,请写出S与x之间的关系式.
答:S=
| 1 |
| 2 |
| 1 |
| 2 |
| 多边形的序号 | ① | ② | ③ | ④ | … |
| 多边形的面积S | 2 | 2.5 | 3 | 4 | … |
| 各边上格点的个数和x | 4 | 5 | 6 | 8 | … |
| 1 |
| 2 |
| 1 |
| 2 |
(3)请你继续探索,当格点多边形内部有且只有N个格点时,猜想S与x有怎样的关系.答:S=
| 1 |
| 2 |
| 1 |
| 2 |
分析:(1)由(1)可以直接得到S=
x;
(2)由图可知多边形内部都有而且只有2格点时,⑤的各边上格点的个数为4,面积为3,⑥的各边上格点的个数为10,面积为6,进而得出答案;
(3)由图可知多边形内部都有而且只有N格点时,面积为:S=
x+(N-1).
| 1 |
| 2 |
(2)由图可知多边形内部都有而且只有2格点时,⑤的各边上格点的个数为4,面积为3,⑥的各边上格点的个数为10,面积为6,进而得出答案;
(3)由图可知多边形内部都有而且只有N格点时,面积为:S=
| 1 |
| 2 |
解答: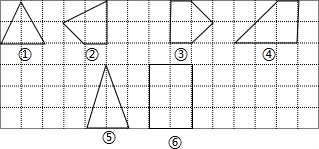 解:(1)∵①各边上格点个数和为:4,S=2,②各边上格点个数和为:5,S=2.5,
解:(1)∵①各边上格点个数和为:4,S=2,②各边上格点个数和为:5,S=2.5,
③各边上格点个数和为:6,S=3,
④各边上格点个数和为:7,S=3.5,
∴S=
x;
(2)由图可知多边形内部都有而且只有2格点时,
⑤的各边上格点的个数为4,面积为3,
⑥的各边上格点的个数为10,面积为6,
∴S=
x+1;
(3)由图可知多边形内部都有而且只有N格点时,面积为:S=
x+(N-1).
故答案为:
x;
x+1;
x+(N-1).
 解:(1)∵①各边上格点个数和为:4,S=2,②各边上格点个数和为:5,S=2.5,
解:(1)∵①各边上格点个数和为:4,S=2,②各边上格点个数和为:5,S=2.5,③各边上格点个数和为:6,S=3,
④各边上格点个数和为:7,S=3.5,
∴S=
| 1 |
| 2 |
(2)由图可知多边形内部都有而且只有2格点时,
⑤的各边上格点的个数为4,面积为3,
⑥的各边上格点的个数为10,面积为6,
∴S=
| 1 |
| 2 |
(3)由图可知多边形内部都有而且只有N格点时,面积为:S=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了图形的变化类,此题需要根据图中表格和自己所算得的数据,总结出规律.寻找规律是一件比较困难的活动,需要仔细观察和大量的验算.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形.设格点多边形的面积为S,它各边上格点的个数和为x.
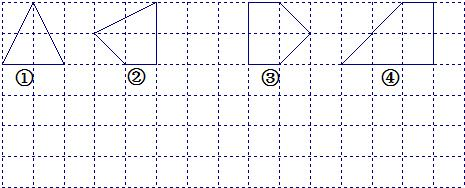
(1)上图中的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请写出S与x之间的关系式;
答:S= .
(2)请你再画出一些格点多边形,使这些多边形内部都有而且只有2格点.此时所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式是:S= ;
(3)请你继续探索,当格点多边形内部有且只有n个格点时,猜想S与x有怎样的关系?
答:S= .

(1)上图中的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请写出S与x之间的关系式;
答:S=
| 多边形的序号 | ① | ② | ③ | ④ | … |
| 多边形的面积S | 2 | 2.5 | 3 | 4 | … |
| 各边上格点的个数和x | 4 | 5 | 6 | 8 | … |
(3)请你继续探索,当格点多边形内部有且只有n个格点时,猜想S与x有怎样的关系?
答:S=
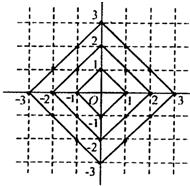 31、用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点..观察图中每一个正方形(实线)四条边上的格点的个数,请回答下列问题:
31、用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点..观察图中每一个正方形(实线)四条边上的格点的个数,请回答下列问题: