题目内容
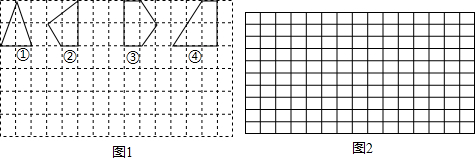
用水平线和竖直线将平面分成若干个边长为1的小正方形格子，小正方形的顶点，叫格点．．观察图中每一个正方形（实线）四条边上的格点的个数，请回答下列问题：
（1）由里向外第1个正方形（实线）四条边上的格点个数共有
（2）由里向外第10个正方形（实线）四条边上的格点个数共有
（3）由里向外第n个正方形（实线）四条边上的格点个数共有
（1）由里向外第1个正方形（实线）四条边上的格点个数共有
4
4
个；由里向外第2个正方形（实线）四条边上的格点个数共有8
8
个；由里向外第3个正方形（实线）四条边上的格点个数共有12
12
个．（2）由里向外第10个正方形（实线）四条边上的格点个数共有
40
40
个．（3）由里向外第n个正方形（实线）四条边上的格点个数共有
4n
4n
个．分析：解这道题时，先固定坐标轴上的四个点，第1个正方形只有坐标轴上的4个点，第2个正方形在每一个象限增加了1个，第3个正方形在每一个象限增加了2个…第n个正方形在每一个象限增加了（n-1）个，发现这一规律，问题自然解决．
解答：解：第1个正方形四条边上的格点共有4个
第2个正方形四条边上的格点个数共有（4+4×1）个
第3个正方形四条边上的格点个数共有（4+4×2）个
… …
第10个正方形四条边上的格点个数共有（4+4×9）=40个
第n个正方形四条边上的格点个数共有[4+4×（n-1）]=4n个．
第2个正方形四条边上的格点个数共有（4+4×1）个
第3个正方形四条边上的格点个数共有（4+4×2）个
… …
第10个正方形四条边上的格点个数共有（4+4×9）=40个
第n个正方形四条边上的格点个数共有[4+4×（n-1）]=4n个．
点评：此题抓住一个不变（坐标轴上的格点）数，另一个有变化规律（每一个象限增加）的数，问题迎刃而解．
练习册系列答案
相关题目
用水平线和竖直线将平面分成若干个边长为1的小正方形格子，小正方形的顶点，叫格点，以格点为顶点的多边形叫格点多边形．设格点多边形的面积为S，它各边上格点的个数和为x．
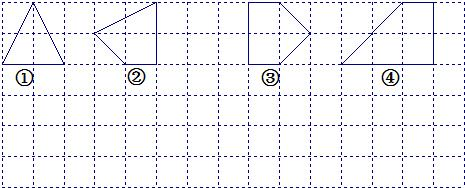
（1）上图中的格点多边形，其内部都只有一个格点，它们的面积与各边上格点的个数和的对应关系如下表，请写出S与x之间的关系式；
答：S= ．
（2）请你再画出一些格点多边形，使这些多边形内部都有而且只有2格点．此时所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式是：S= ；
（3）请你继续探索，当格点多边形内部有且只有n个格点时，猜想S与x有怎样的关系？
答：S= ．
（1）上图中的格点多边形，其内部都只有一个格点，它们的面积与各边上格点的个数和的对应关系如下表，请写出S与x之间的关系式；
答：S=
| 多边形的序号 | ① | ② | ③ | ④ | … |
| 多边形的面积S | 2 | 2.5 | 3 | 4 | … |
| 各边上格点的个数和x | 4 | 5 | 6 | 8 | … |
（3）请你继续探索，当格点多边形内部有且只有n个格点时，猜想S与x有怎样的关系？
答：S=
