题目内容
在Rt△ABC中,AB=k·AC,∠BAC=90°,AD⊥BC,点M为 BC上任意一点,MF⊥AB于F,ME⊥AC于E,连接DE、DF。
(1)如图 1,当k=1时,观察、测量、猜想DF与DE之间的数量关系为_________,位置关系为_____________ 。
(2)如图2,当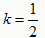 时(1)中的结论是否还成立?若成立,写出证明过程;若不成立,说明理由。
时(1)中的结论是否还成立?若成立,写出证明过程;若不成立,说明理由。
(3)猜想:当k=n时,DF与DE之间的数量关系为___________。
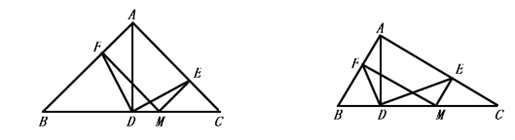
图1 图2
解:( 1 ) DF=DE DF⊥DE
(2)第一个结论不成立,第二个结论成立.
理由:
∵k=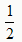 ,AB=
,AB=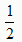 AC,
AC,
∵∠BAC=90°,AD⊥BC
∴AD=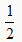 CD,∠FAD=∠DCE
CD,∠FAD=∠DCE
因为MF⊥AB,ME⊥AC,
四边形AFME 为矩形,
AMEC 为直角三角形,
AF=ME=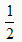 CE,
CE,
∴△DCE∽△DAF,
所以DF=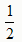 DE
DE
∵∠EDC=∠FDA,∠ADE+∠EDC=90°,
∴∠FDA+∠EDA=90°,
∴DE⊥DF
(3)DF=nDE
(2)第一个结论不成立,第二个结论成立.
理由:
∵k=
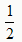 ,AB=
,AB=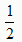 AC,
AC,∵∠BAC=90°,AD⊥BC
∴AD=
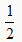 CD,∠FAD=∠DCE
CD,∠FAD=∠DCE因为MF⊥AB,ME⊥AC,
四边形AFME 为矩形,
AMEC 为直角三角形,
AF=ME=
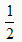 CE,
CE,∴△DCE∽△DAF,
所以DF=
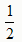 DE
DE ∵∠EDC=∠FDA,∠ADE+∠EDC=90°,
∴∠FDA+∠EDA=90°,
∴DE⊥DF
(3)DF=nDE

练习册系列答案
相关题目
在Rt△ABC中,已知a及∠A,则斜边应为( )
| A、asinA | ||
B、
| ||
| C、acosA | ||
D、
|
 如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )
如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )| A、9:4 | B、9:2 | C、3:4 | D、3:2 |
 已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径.
已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径. 如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )
如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )