题目内容
二次函数y=x2-4x+3的图象交x轴于A、B两点，交y轴于点C，△ABC的面积为________．
3
分析：由二次函数y=x2-4x+3求出A、B两点的x轴坐标，再求出C点的y轴坐标，根据面积公式就解决了．
解答：由表达式y=x2-4x+3=（x-1）×（x-3），
则与x轴坐标为：A（1，0），B（3，0），
令x=0，得y=3，即C（0，3）
∴△ABC的面积为：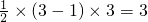
．
点评：此题考查二次函数和三角形的基本性质，求出三点坐标后问题就解决了．
分析：由二次函数y=x2-4x+3求出A、B两点的x轴坐标，再求出C点的y轴坐标，根据面积公式就解决了．
解答：由表达式y=x2-4x+3=（x-1）×（x-3），
则与x轴坐标为：A（1，0），B（3，0），
令x=0，得y=3，即C（0，3）
∴△ABC的面积为：
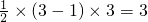．点评：此题考查二次函数和三角形的基本性质，求出三点坐标后问题就解决了．
练习册系列答案
相关题目