题目内容
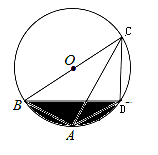
【题目】如图，四边形ABCD内接于⊙O，BC是直径，∠BAD=120°，AB=AD.
(1)、求证：四边形ABCD是等腰梯形；(2)、已知AC=6，求阴影部分的面积.
【答案】(1)、证明过程见解析(2)、4π－3
【解析】
试题分析：(1)根据AB=AD，∠BAD=120°可以得到∠ABD=∠ADB=30°，从而说明弧AB和弧AD的度数为60°，根据BC为直径可以说明弧CD的度数也是60°，从而可以得到AB=CD，然后根据∠CAD=∠ACB=30°得出AD∥BC；(2)、阴影部分面积利用扇形面积减去△BOD的面积.
试题解析：⑴、∵∠BAD=120°，AB=AD ∴∠ABD=∠ADB=30° ∴弧AB和弧AD的度数都等于60°
又 ∵BC是直径 ∴弧CD的度数也是60°∴AB=CD
∵∠CAD=∠ACB=30°∴BC∥AD ∴四边形ABCD是等腰梯形.
⑵、∵BC是直径 ∴∠BAC=90° ∵∠ACB=30°，AC=6∴BC=
∴r=2
∵弧AB和弧AD的度数都等于60°∴∠BOD=120°
连接OA交BD于点E,则OA⊥BD ∴OE=OB×sin30°= BE=0B×cos30°=3BD=2BE=6
∴
=
=4π－3.
练习册系列答案
相关题目
