题目内容
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
①∠EBG=45°;②△DEF∽△ABG;③S△ABG= ![]() S△FGH;④AG+DF=FG.
S△FGH;④AG+DF=FG.
其中正确的是 . (把所有正确结论的序号都选上)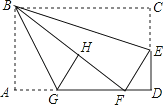
【答案】①③④
【解析】解: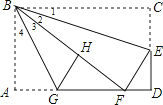
∵△BCE沿BE折叠,点C恰落在边AD上的点F处,
∴∠1=∠2,CE=FE,BF=BC=10,
在Rt△ABF中,∵AB=6,BF=10,
∴AF= ![]() =8,
=8,
∴DF=AD﹣AF=10﹣8=2,
设EF=x,则CE=x,DE=CD﹣CE=6﹣x,
在Rt△DEF中,∵DE2+DF2=EF2 ,
∴(6﹣x)2+22=x2 , 解得x= ![]() ,
,
∴ED= ![]() ,
,
∵△ABG沿BG折叠,点A恰落在线段BF上的点H处,
∴∠3=∠4,BH=BA=6,AG=HG,
∴∠2+∠3= ![]() ∠ABC=45°,所以①正确;
∠ABC=45°,所以①正确;
HF=BF﹣BH=10﹣6=4,
设AG=y,则GH=y,GF=8﹣y,
在Rt△HGF中,∵GH2+HF2=GF2 ,
∴y2+42=(8﹣y)2 , 解得y=3,
∴AG=GH=3,GF=5,
∵∠A=∠D, ![]() =
= ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴ ![]() ≠
≠ ![]() ,
,
∴△ABG与△DEF不相似,所以②错误;
∵S△ABG= ![]() 63=9,S△FGH=
63=9,S△FGH= ![]() GHHF=
GHHF= ![]() ×3×4=6,
×3×4=6,
∴S△ABG= ![]() S△FGH , 所以③正确;
S△FGH , 所以③正确;
∵AG+DF=3+2=5,而GF=5,
∴AG+DF=GF,所以④正确.
所以答案是①③④.
【考点精析】解答此题的关键在于理解相似图形的相关知识,掌握形状相同,大小不一定相同(放大或缩小);判定:①平行;②两角相等;③两边对应成比例,夹角相等;④三边对应成比例.

 名校课堂系列答案
名校课堂系列答案【题目】某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)
选修课 | A | B | C | D | E | F |
人数 | 40 | 60 | 100 |
根据图表提供的信息,下列结论错误的是( )
A.这次被调查的学生人数为400人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中喜欢选修课E,F的人数分别为80,70
D.喜欢选修课C的人数最少