题目内容
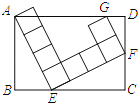
【题目】如图,矩形ABCD中,由8个面积均为1的小正方形组成的L型模板如图放置,则矩形ABCD的周长为( )
A.12![]() B.10
B.10![]() C.8
C.8![]() D.8+4
D.8+4![]()
【答案】C
【解析】
可设BE=x,CE=y,由题意可得△ABE≌ECF,并且△ECF∽△FDG,从而得出关于x、y的两个方程,求解后即可得出矩形ABCD的周长;
解:∵小正方形的面积为1,
∴小正方形的边长也为1,
设BE=x,CE=y,
∵∠AEB+∠CEF=90°,而∠EFC+∠CEF=90°,
∴∠AEB=∠EFC,
又∵∠B=∠C=90°,AE=EF=4,
∴△ABE≌ECF(AAS),
∴AB=EC=y,BE=CF=x,
∴由勾股定理可得x2+y2=42,
而同理可得∠EFC=∠FGD,且∠C=∠D=90°,
∴△ECF∽△FDG,
∴![]() ,
,
∴FD=![]() EC=
EC=![]() y,
y,
∵AB=CD,
∴y=x+![]() y,
y,
∴y=2x,将其代入x2+y2=42中
于是可得x=![]() ,y=
,y=![]() ,
,
而矩形ABCD的周长=2(x+y)+2y=5y=5×![]() =
= ![]() ;
;
故选:C.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目