题目内容
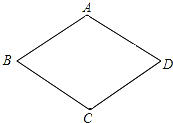
【题目】已知ABCD的一组邻边AB、AD的长是关于x的方程x2﹣4x+m=0的两个实根.
(1)当m为何值时,四边形ABCD是菱形?
(2)在第(1)问的前提下,若∠ABC=60°,求ABCD的面积.
【答案】(1)当m=4时,四边形ABCD是菱形;(2)2![]() .
.
【解析】
试题分析:(1)四边形ABCD是菱形时,AB=AD,由一元二次方程根的判别式=0即可求出m的值;
(2)连接AC、BD交于点O,由一元二次方程的根求出AB的长,进一步利用菱形的性质和30°角的直角三角形的性质求得对角线的长,利用面积计算方法计算得出答案即可.
解:(1)四边形ABCD是菱形时,AB=AD,
∵AB,AD的长是关于x的方程x2﹣mx+4=0的两个实数根,
∴△=(﹣4)2﹣4m=0,
解得:m=4,
∴当m=4时,四边形ABCD是菱形
(2)如图,连接AC、BD交于点O,
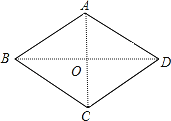
当m=4时,
x2﹣4x+4=0,
解得:x1=x2=2,
则AB=2,
∵四边形ABCD是菱形,∠ABC=60°,
∴∠ABO=![]() ∠ABC=30°,
∠ABC=30°,
D═2OB,AC=2OA,AC⊥BD,
在直角△AOB中,
∵∠ABO=30°,
∴OA=![]() AB=1,
AB=1,
0B=![]() ,
,
BD=2OB=2![]() ,
,
AC=2OA=2,
∴S菱形ABCD=![]() BDAC=
BDAC=![]() ×2×2
×2×2![]() =2
=2![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目