题目内容
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.
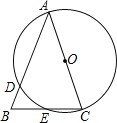
(1)求证:BE=CE;
(2)若BD=2,BE=3,求AC的长.
【答案】(1)见解析;(2)9.
【解析】
试题分析:(1)连结AE,如图,根据圆周角定理,由AC为⊙O的直径得到∠AEC=90°,然后利用等腰三角形的性质即可得到BE=CE;
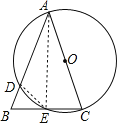
(2)连结DE,如图,证明△BED∽△BAC,然后利用相似比可计算出AB的长,从而得到AC的长.
(1)证明:连结AE,如图,
∵AC为⊙O的直径,
∴∠AEC=90°,
∴AE⊥BC,
而AB=AC,
∴BE=CE;
(2)连结DE,如图,
∵BE=CE=3,
∴BC=6,
∵∠BED=∠BAC,
而∠DBE=∠CBA,
∴△BED∽△BAC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴BA=9,
∴AC=BA=9.

练习册系列答案
相关题目