题目内容
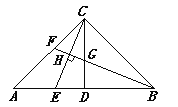
【题目】如图,在△ABC中,CD是中线,∠ACB=90°,AC=BC,点E,F分别为AB,AC上的动点(均不与端点重合),且CE⊥BF,垂足为H,BF与CD相交于G.
(1)求证:AE=CG;
(2)当线段AE,CF之间满足什么数量关系时,BF为△ABC的角平分线?请说明理由.
【答案】(1)证明见解析;(2)当AE=CF时,BF为△ABC的角平分线.理由见解析.
【解析】试题分析:
(1)由等腰直角三角形的性质可证得∠A=∠BCG=45°,再由∠ACE+∠BCE=90°,∠CBG+∠BCE=90°,得到∠ACE=∠CBG,这样结合AC=BC,由“ASA”可证△ACE≌△CBG就可得到结论了;
(2)当AE=CF时,BF是△ABC的角平分线;由AE=CF,AE=CG,可得CF=CG,这样∠CFG=∠CGF,进一步就可证得∠CBF=∠DBF,从而可得BF平分∠ABC.
试题解析:
(1)∵∠ACB=90°,AC=BC,CD是中线,
∴∠ACE+∠BCE=90°,∠A=∠ABC=∠BCG=45°.
∵CE⊥BF,垂足为H,∴∠BHC=90°.
∴∠CBG+∠BCE=90°.
∴∠ACE=∠CBG.
在△ACE和△CBG中: 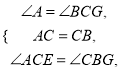
∴△ACE≌△CBG.
∴AE=CG.
(2)当AE=CF时,BF为△ABC的角平分线.
理由如下:∵AE=CF,AE=CG.
∴CF=CG.
∴∠CFG=∠CGF.
∵∠CFG=∠A+∠ABF,∠CGF=∠BCG+∠CBF,∠A=∠BCG,
∴∠ABF=∠CBF.即BF为△ABC的角平分线.

练习册系列答案
相关题目